Решить логарифмическое уравнение
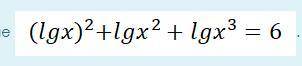
Другие вопросы по теме Математика
Популярные вопросы
- Франко.І. Коли ще звірі говорили літературний паспорт Головні герої:Другорядні...
2 - з деякої точки простору до площини дві поході проекції, які дозволяють...
2 - Какидтсииидиитие виды семян...
1 - з деякої точки простору до площини дві поході проекції, які дорівнюють...
2 - как читается это число 1183120000,00...
3 - Решите 1. He English 2. They tall and thin 3. Lucy Italian 4. We...
2 - Знайдіть значення функції у=6/х, якщо х=1,5...
3 - Why are metalli oxide called basic oxide...
2 - мне ежелги адамдар туралы малимет керк тез?...
3 - Решить уравнение с параметром...
2
x1=10;. x2=1/10^6
Пошаговое объяснение:
lg²(x) + lg(x^2) + lg(x^3) = 6 =>
=> lg²(x) +lg(x^5)=6 степень х^5 перекинем вперёд => 5lg(x);
lg²(x)+5lg(x)-6 = 0 отметим lg(x)=t
t²+5t-6=0
(t-1)×(t+6)=0 => t1=1; t2=-6
lg(x)=1;. lg(x)=-6
x1=10. x2=10^(-6) => 1/10^6
Смотри........................