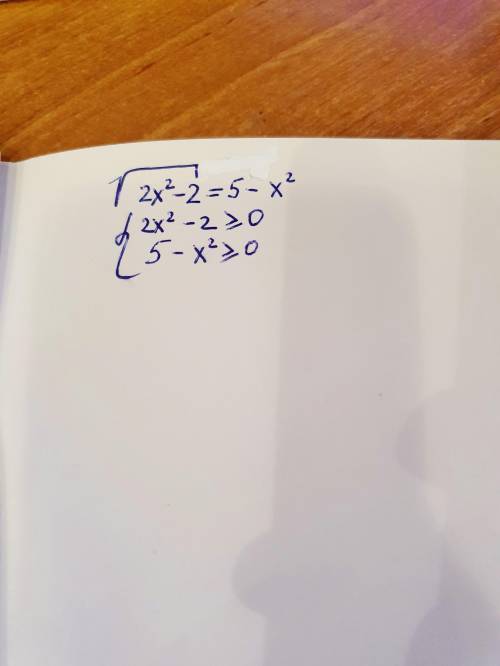
Математика: решить иррациональное уравнение

Пошаговое объяснение:ОДЗ:Решим оба неравенства методом интервалов.Нули функции:Найдём знаки неравенства на промежуткахНули функции:Найдём знаки неравенства на промежуткахИтого:Введём замену:Перепишем уравнение с учётом замены:Решаем уравнение по теореме Виета:Вернёмся к замене:Корни x₃ и x₄ не удовлетворяют ОДЗ, так какОстаются корни x₁ и x₂ ....

решить иррациональное уравнение

Ответы

Kardeyv 12.01.2021 16:25

$\pm \sqrt{3}$

Пошаговое объяснение:

ОДЗ:

$\left \{ {{2x^{2}-2 \geq 0} \atop {5-x^{2} \geq 0}} \right. \Leftrightarrow \left \{ {{x^{2}-1 \geq 0} \atop {x^{2}-5 \leq 0}} \right. \Leftrightarrow \left \{ {{(x-1)(x+1) \geq 0} \atop {(x-\sqrt{5})(x+\sqrt{5}) \leq 0}} \right. ;$

Решим оба неравенства методом интервалов.

$(x-1)(x+1) \geq 0;$

Нули функции:

(x-1)(x+1)=0;

$x=1 \quad \vee \quad x=-1;$

Найдём знаки неравенства на промежутках

$(-\infty; -1], \quad [-1; 1], \quad [1; +\infty);$

$x=-2 \Rightarrow (-2-1)(-2+1)=-3 \cdot (-1)=30;$

$x=0 \Rightarrow (0-1)(0+1)=-1 \cdot 1=-1$

$x=2 \Rightarrow (2-1)(2+1)=1 \cdot 3=30;$

$x \in (-\infty; -1] \cup [1; +\infty);$

$(x-\sqrt{5})(x+\sqrt{5}) \leq 0;$

Нули функции:

$(x-\sqrt{5})(x+\sqrt{5})=0;$

$x=\sqrt{5} \quad \vee \quad x=-\sqrt{5};$

Найдём знаки неравенства на промежутках

$(-\infty; -\sqrt{5}], \quad [-\sqrt{5}; \sqrt{5}], \quad [\sqrt{5}; +\infty);$

$x=-3 \Rightarrow (-3-\sqrt{5})(-3+\sqrt{5})=(-3)^{2}-(\sqrt{5})^{2}=9-5=40;$

$x=0 \Rightarrow (0-\sqrt{5})(0+\sqrt{5})=-\sqrt{5} \cdot \sqrt{5}=-5$

$x=3 \Rightarrow (3-\sqrt{5})(3+\sqrt{5})=3^{2}-(\sqrt{5})^{2}=9-5=40;$

$x \in [-\sqrt{5}; \sqrt{5}];$

Итого:

$x \in [-\sqrt{5}; -1] \cup [1; \sqrt{5}];$

$\sqrt{2x^{2}-2}=5-x^{2};$

$(\sqrt{2x^{2}-2})^{2}=(5-x^{2})^{2};$

$25-10x^{2}+(x^{2})^{2}=2x^{2}-2;$

$(x^{2})^{2}-10x^{2}-2x^{2}+25+2=0;$

$(x^{2})^{2}-12x^{2}+27=0;$

Введём замену:

$t=x^{2};$

Перепишем уравнение с учётом замены:

$t^{2}-12t+27=0;$

Решаем уравнение по теореме Виета:

$\left \{ {{t_{1}+t_{2}=-(-12)} \atop {t_{1} \cdot t_{2}=27}} \right. \Leftrightarrow \left \{ {{t_{1}+t_{2}=12} \atop {t_{1} \cdot t_{2}=27}} \right. \Leftrightarrow \left \{ {{t_{1}=3} \atop {t_{2}=9}} \right. ;$