1. Математика
  2. Решить алгебраическим и

Решить алгебраическим и подставным


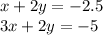
x + 2y = - 2.5 \\ 3x + 2y = - 5

сснсогаоаг сснсогаоаг    2   10.09.2021 01:22    0

Ответы
ishnlv ishnlv  26.11.2021 01:53

x + 2y = - 2.5,

3x + 2y = - 5

сложения. Нам нужно сделать так, чтобы при сложении какая-то из переменных исчезла. Модуль переменной дожен быть равен в двух уравнениях, а знаки разные. Нужно выбрать любую из переменных. Тут проще взять 2y. Необходимо, чтобы в одном уравнении было 2y, а в другом — -2y. Для этого домножим одно из уравнений на -1.

x + 2y = - 2.5 | \times ( - 1),

3x + 2y = - 5;

- x - 2y = 2.5,

3x + 2y = - 5;

Теперь можно сложить.

- x + 3x - 2y + 2y = 2.5 - 5

2x = - 2.5

x = - 1.25

Одна из переменной известна. Нужно подставить это значение в любое из уравнений системы.

x + 2y = - 2.5

- 1.25 + 2y = - 2.5

2y = - 1.25

y = - 0.625

ответ: –1.25; –0.625

подстановки. Метод заключается в том, что нужно выразить переменную из одного уравнения и подставить другое. Тут, опять же, проще начать с первого уравнения. Выразим x.

x = - 2.5 - 2y

Теперь подставляем во второе уравнение.

3( - 2.5 - 2y) + 2y = - 5

- 7.5 - 6y + 2y = - 5

- 4y = 2.5

y = - 0.625

Полученное значение y подставляем в первое выражение.

x = - 2.5 - 2 \times ( - 0.625) = - 1.25

ответ: –1.25; – 0.625

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
goldin1337 goldin1337  16.04.2020 13:45
Жүк машинасы 1,5 сағат 50 км/сағ жылдамдықпен, 54 км/сағ жылдамдықпен 2,5 сағ және 54 км/сағ жылдамдықпен 2 сағ жүрді. Жүк машинасының орташа жылдамдығын тап....
trofimovigor07 trofimovigor07  16.04.2020 13:45
На фотці завдання Будь ласка виконайте...
ksenia112005 ksenia112005  16.04.2020 13:45
буду нереально благодарна ​...
автормемов автормемов  16.04.2020 13:45
Треугольник авс задан координатами своих вершин a(1,4,6) b(-2,-3,5) С(-3,-4,-5) А)постройте указанный треугольник Б)Найдите косинус угла В...
tamilatumasheva tamilatumasheva  16.04.2020 13:45
В конкурсе участвовало 60 школьников семь двенадцатых из них девочки сколько девочек участвовало в конкурсе?распишите по действиям заранее...
тупая761 тупая761  16.04.2020 13:45
ответьте следующие точки (0,5),(2,2),(6,-3),(8,-4),(10,-2),(12,2),(14,6),(16,8),(18,5),(20,4),(22,3),(24,3).Соедините точки непрерывной линией...
КАТЯ3105 КАТЯ3105  16.04.2020 13:45
5x+8=8x+23 уравнение решить пошагово...
Lusi28 Lusi28  16.04.2020 13:45
Килограм апельсинов дороже чем килограм яблок на 6.4грн. За 5 кг апельсинов заплатили стокоже сколько и за 9 кг яблок. Сколько стоит 1 кг апельсинов и 1 кг яблок?...
YummyGirl YummyGirl  16.04.2020 13:45
Решите эти 3 уравнения дам...
ilonasuper ilonasuper  16.04.2020 13:45
Найдите объём прямоугольного параллепипеда , если площадь нижнего основания равно 23см в квадрате, a его высота 60мм...

Популярные вопросы