РЕБЯТ РЕШИТЕ ОЧЕНЬ НАДООО НИЖНЕЕ САМОЕ ГДЕ ТАМ УПРАЖНЕНИЯ И ЗАДАЧИ РЕШИТЬ НА МНОЖЕСТВЕ R неравенства

Пошаговое объяснение:

А)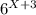 >36 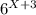    > 6² основание 6 >1   , функция возрастающая, значит х+3>2   x>2-3   x> -1  Отв: х∈(-1;+∞)                                                   б) (1/5)ˣ⁺⁴<1/125    (1/5)ˣ⁺⁴<(1/5)³   основание 0< 1/5<1, функция убывающая, значит х+4>3   x>3-4   x>-1   Отв: х∈(-1;+∞)                              в)(5)ˣ²⁺ˣ > 1   (5)ˣ²⁺ˣ > 5⁰   основание 5>1, значит функция возрастающая, х²+х>0    x(x+1)>0   x∈(-∞;-1)∪(0;+∞)                                        г)2ˣ²⁻ˣ⁺⁸>0 неравенство верно при любом х, т.к. показательная функция всегда положительна Отв: (-∞;+∞)                                                    д) (0,3)ˣ⁺⁵<-4 ,показательная функция всегда положительна, поэтому неравенство не имеет решения Отв: ∅                                                          е) 2ˣ ·5ˣ ≤0, 001·(10ˣ⁻²)³    2ˣ ·5ˣ ≤ 10⁻² · (10ˣ⁻²)³    10ˣ ≤ 10⁻² · (10)³ˣ⁻⁶                    10ˣ ≤10³ˣ⁻⁸, основание 10>1, значит х<3x-8     -2x<-8  x>4 Отв (4:+∞)                           ж) 2ˣ⁺²-2ˣ⁺³ -2ˣ⁺⁴ >5ˣ⁺¹ -5ˣ⁺²      2ˣ⁺²(1-2-4) > 5ˣ⁺¹(1-5)     2ˣ⁺² ·(-5 )> 5ˣ⁺¹· (-4)           2ˣ⁺² : 4 > 5ˣ⁺¹:5    2ˣ⁺> 5ˣ, разделим обе части неравенства на  5ˣ>0, тогда (2/5)ˣ > 1,   (2/5)ˣ >(2/5)⁰, основание 0<(2/5)<1. Значит функция убывающая, поэтому х< 0   Отв: (-∞;0)