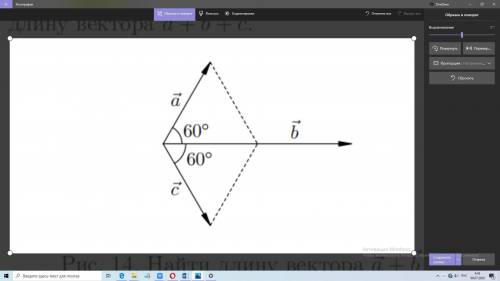
Пусть длины векторов a и c равны 1, длина вектора b равна 2; угол между векторами a и b равен 60°, угол между векторами b и c тоже равен 60°. Требуется найти длину вектора a +b + c.

Давайте разберемся с данным вопросом. У нас есть три вектора: a, b и c. Длина вектора a и c равна 1, а длина вектора b равна 2. Угол между векторами a и b равен 60°, а угол между векторами b и c тоже равен 60°. Мы хотим найти длину вектора a + b + c.

Для решения этой задачи, воспользуемся свойствами векторов и тригонометрии.

Шаг 1: Найдем компоненты вектора b относительно осей x и y. Так как длина вектора b равна 2, а угол между вектором b и осью x равен 60°, мы можем использовать тригонометрию чтобы найти эти компоненты.

Мы знаем, что b_x = b * cos(theta), где b_x - компонента вектора b по оси x, b - длина вектора b, а theta - угол между вектором b и осью x.

b_x = 2 * cos(60°) = 2 * 1/2 = 1

Аналогично, b_y = b * sin(theta), где b_y - компонента вектора b по оси y, а sin(theta) - синус угла между вектором b и осью y.

b_y = 2 * sin(60°) = 2 * √3/2 = √3

Таким образом, компоненты вектора b равны b_x = 1 и b_y = √3.

Шаг 2: Теперь найдем компоненты векторов a и c. Поскольку их длины равны 1, они представляют собой векторы с постоянной длиной, так что их компоненты будут пропорциональны компонентам вектора b.

Поскольку угол между векторами a и b равен 60°, мы можем использовать тот факт, что косинус угла между двумя векторами равен отношению скалярного произведения этих векторов к произведению их длин.

cos(theta) = (a * b) / (|a| * |b|)

Для векторов a и b:

cos(60°) = (a * b) / (1 * 2)

1/2 = a * 1 / 2

a = 1/2

Аналогично, компоненты вектора c также равны 1/2.

Таким образом, компоненты векторов a и c равны a_x = 1/2, a_y = √3/2 и c_x = 1/2, c_y = √3/2.

Шаг 3: Теперь сложим компоненты векторов a, b и c, чтобы найти компоненты вектора a + b + c.

(a + b + c)_x = a_x + b_x + c_x = 1/2 + 1 + 1/2 = 2

(a + b + c)_y = a_y + b_y + c_y = √3/2 + √3 + √3/2 = √3 + √3 = 2√3

Таким образом, компоненты вектора a + b + c равны (a + b + c)_x = 2 и (a + b + c)_y = 2√3.

Шаг 4: Найдем длину вектора a + b + c, используя теорему Пифагора.

|a + b + c| = √((a + b + c)_x^2 + (a + b + c)_y^2) = √(2^2 + (2√3)^2) = √(4 + 12) = √16 = 4

Таким образом, длина вектора a + b + c равна 4.

Ответ: Длина вектора a + b + c равна 4.