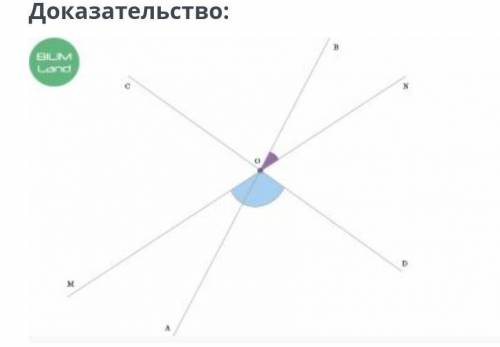
Прямые AB, CD и MN пересекаются в точке O. Известно, что ∠MOD составляет 60% от градусной меры угла COD, а угол BON составляет 25% от градусной меры угла DON. Докажи, что AB ⊥ CD.
Доказательство:

(Нужно выстроить верный порядок, передвигая строки вверх-вниз)
Углы ∠MOD и ∠DON – смежные ⇒
то ∠BON = 72° · 0,25 = 18°.
то ∠COD = 180°. Так как 60% = 0.6,
⇒ ∠DON = ∠MON – ∠MOD = 180° – 108° = 72°.
Следовательно, ∠BOD =∠DON + ∠BON = 72° + 18° = 90°.
Так как ∠COD – развернутый,
то ∠MOD = 180° · 0,6 = 108°.
А если ∠BON составляет 25% от ∠DON,
Если ∠BOD = 90°, то AB ⊥ CD.​

Andrianovnd    3   27.10.2020 14:41    1