Решить по ! без использования тригонометрические функций!

Проведём перпендикуляр OH к AC.

Рассмотрим ΔAMK и ΔAHO:

⇒ ΔAMK ~ ΔAHO по двум углам ⇒

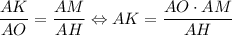
ΔAOC — равнобедренный, OH ⊥ AC ⇒ AH = HC ⇒ AH = AC : 2 = 3.

O — центр пересечения биссектрис, но ΔABC — правильный ⇒ O — точка пересечения медиан (которые в правильном треугольнике равны, как бы их ни проводили; обозначим медиану за m) ⇒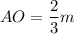 . Но в правильном треугольнике медиана — это ещё и высота, значит, .

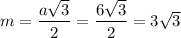ответ: AK = 2 см, KC = 4 см