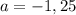При каком значении параметра a касательная к графику функции y=ax2+4x+3 в точке x=2 образует с осью x угол 135°?
Другие вопросы по теме Математика
Популярные вопросы
- 1. в электронных таблицах осуществить копирование формулы, содержащей...
1 - Определите площадь полной поверхности куба, если расстояние между...
2 - Почему рене декарт назвал абсциссу абсциссой а ординату ординатой...
1 - Розібрати слова за будовою : розшукати, жнива, безпорядок, весело,сніг,...
2 - Какие поговорки подойдут к сказке п. п. бажова серебряное копытце...
2 - Сколько звуков а в словах: утка, стая ,якоря ,змея ,ворон ,дятел....
2 - Умоляю ! шар массой 1 кг, движущийся со скоростью 10 м/с, ударяется...
3 - Полипептид состоит из 20 аминокислот. определите число нуклеотидов...
2 - Сочинение в.с.гросман жизнь и судьба...
3 - Сделать звукобуквенный разбор слова чудесный...
2
Имеем квадратичную функцию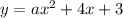
Воспользуемся геометрическим смыслом производной: производная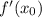 в точке с абсциссой
в точке с абсциссой 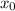 функции
функции 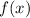 численно равна тангенсу угла наклона касательной, проведенной к данной точке.
численно равна тангенсу угла наклона касательной, проведенной к данной точке.
Найдем производную функции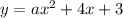 :
:
Найдем значение производной в точке с абсциссой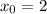 :
:
Используем геометрический смысл производной: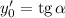
Таким образом, если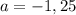 касательная к графику функции
касательная к графику функции 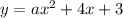 в точке
в точке 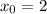 образует с осью x угол
образует с осью x угол 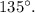
ответ: