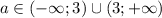При каких значениях α прямые αx-2y-1=0 и 6x-4y-3=0
а) Параллельны
б) Имеют одну общую точку
Другие вопросы по теме Математика
Популярные вопросы
- Проблематика твору місце для дракона...
3 - Рассуждение по теме: самая главная формула успеха - знание,как обращаться...
2 - Дайте оценку административным преобразованиям конца 1950-х начала 1960-х гг...
2 - Допиши речення.хати не маєте,а двері ос., мн., теп. ч.)...
1 - Открой обратный словарь на й просмотри списки слов на жий на ший и на щий....
2 - Какие человеческие качества лёньке найти себя в жизни? в чем проявились его...
2 - Сочинение-рассуждение на тему книга - мой друг !...
2 - Определите частоту колебаний вибратора , если длина волны 10 м , а скорость...
2 - Пешеход и велосипедист двигаются из города а в город б. пешеход это расстояние...
1 - Однокоренными могут быть и и предложения !...
1
а) Если даны две функции, у которых коэффициент k (стоящий перед x) равен, то графики этих функций будут параллельны.
У первой функции k = a/2, у второй - 1,5. Для того, чтобы коэффициенты были равны, нужно подставить такое значение a, чтобы при делении на 2 оно давало 1,5.
В таком случае, a = 3.
б) Если даны две функции, не имеющих равных коэффициентов k и m (то есть она не будут параллельны или одна функция не равна другой), то у графиков этих функций будет одна общая точка. В таком случае, a может принять любое значение, кроме 3 (иначе графики будут параллельны).
То есть,