При каких значениях переменной x имеет смысл выражение 2/корень из x-5
Другие вопросы по теме Математика
Популярные вопросы
- Какие чувства испытывает тарас при убийстве сына?...
1 - Составь формулу соединения кальция с азотом (степень окисления -3) и найди его...
3 - Укажи вид птиц который обустраивает гнезда в норах на северном побережье атлантики...
1 - Решите линейное уравнение: 8(3s+7)−10(2s+6)=−4s+19...
1 - Ахаракткризуйте и оцените леонардо да винчи. не менее 20 предл. лексика и тд. 7...
3 - F(x)=cos2x+3x 2+9 найти производную функции по определению...
3 - Какое проверочное слово к слову мальчиков?...
2 - Як поводилися матроси і капітан у смертельно небезпечній ситуації?...
1 - (если что я украинка пишу на руском не люди решыть логическую нам училка задала...
2 - Периметр треугольника abc равен 54см. сторона bc больше стороны ab в 2 целых 2/5...
1
x∈(5; +∞)
Пошаговое объяснение:
Есть выражение: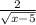 .
.
1) Для того, чтобы корень имела смысл подкоренное выражение должен быть неотрицательным, то есть x-5≥0.
2) Для того, чтобы дробь имела смысл, надо чтобы знаменатель был отличен от нуля. В нашем случае знаменатель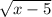 и чтобы он был отличен от нуля х не должно ровняться 5.
и чтобы он был отличен от нуля х не должно ровняться 5.
Если объединит оба требования, то получим: x>5
(5;+∞)
Пошаговое объяснение:
Так как арифметический квадратный корень определен на множестве неотрицательных чисел и знаменатель дроби отличен от нуля, то найдем при каких значениях имеет смысл выражение , решив неравенство:
Значит x∈ ( 5; +∞).