Представить в тригонометрической форме числа(50Б)
Другие вопросы по теме Математика
Популярные вопросы
- Главная мысль сказки сундук самолёт...
2 - Вероятность того, что на тестировании по учащийся а. верно решит больше 9...
3 - Турист может пообедать в 3 столовых города. вероятность того, что он отправится...
3 - Сна delphi пусть дана вещественная квадратная матрица порядка n. относительно...
3 - Впрямоугольном треугольнике abc : ac=6, tgbac=2√2. найдите длину гипотенузы...
1 - Отппвьте сочинение на тему мой любимый предмет...
2 - Сторона ромба з гострим кутом 30градусів =12см. знайти s ромба...
2 - Подготовьте рассказ о животных и растениях вашего края....
2 - Визначте абсолютний показник заломлення середовища, якщо кут падіння променів...
3 - Решить ! от пристани, где скорость течения москвы - реки равна 4 км/ч, одновременно...
1
Пошаговое объяснение:
для z = a + bi => z = |z|*(cos(α) + i*sin(α))
поэтому:
1) |z| = √(1^2 + 1^2) = √2
α = arctg(b/a) = arctg 1 =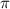 /4
/4
z = √2 * (cos(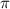 /4) + i*sin(
/4) + i*sin(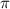 /4))
/4))
2) |z| = √((-3)^2 + (-1)^2) = √10
α = arctg(b/a) = arctg √3 =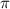 /3
/3
z = √10 * (cos(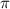 /3) + i*sin(
/3) + i*sin(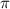 /3))
/3))
3) |z| = √((0)^2 + (2)^2) = 2
α = arctg(b/a) = arctg ∞ (грубо т.к. на самом деле 2/0 это неопределенность) =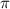 /2
/2
z = 2 * (cos(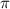 /2) + i*sin(
/2) + i*sin(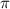 /2))
/2))
4) |z| = √((-5)^2 + (0)^2) = 5
α = arctg(b/a) = arctg 0 = 0
z = √10 * (cos(0) + i*sin(0))