Постройте график функции y=2x^2+8x+2; найдите: а) значение y при x=-2,3 -0,5 1,2; б) значения x,при которых y=-4, y=-1, y=1,7; в)нули функции и промежитки, где y> 0, y < 0; г)область значений. все подробно .

Ответы

диди21 06.10.2020 19:58

Упростим функцию к виду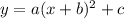 y=a(x+b)^2+c , где (-b;c) - координаты вершины параболы.

y=2x^2+8x+2=2(x^2+4x+1)=2(x^2+4x+4-3)=2(x+2)^2-6

Имеем (-2;-6) - координаты вершины параболы, ветви направлены вверх.

a) Подставим значение аргумента x в график уравнения, получим

$x=-2.3;~~~ y=2(-2.3+2)^2-6=-5.82\\ x=-0.5;~~~ y=2(-0.5+2)^2-6=-1.5\\ x=1.2;~~~~~y=2(1.2+2)^2-6=14.48$

б) Аналогично подставляем значения функций в график уравнения, получим значение аргумента х

$y=-4;~~ -4=2(x+2)^2-6~~\Rightarrow~~ (x+2)^2=1~~\Rightarrow~~ x+2=\pm 1\\ \\~~~~~~~~~~~~~~~~x_1=-1;~~~~ x_2=-3$

$y=-1;~~~\Rightarrow~~ -1=2(x+2)^2-6~~~\Rightarrow~~~ (x+2)^2=2.5\\ \\~~~~~~~~x+2=\pm\sqrt{2.5}~~~~~\Rightarrow~~~~ x_{1,2}=-2\pm\sqrt{2.5}$

$y=1.7;~~ 1.7=2(x+2)^2-6~~~\Rightarrow~~~3.85=(x+2)^2~~~\Rightarrow~~ x+2=\pm\sqrt{3.85}\\ \\ ~~~~~~~~~~~~~~~~~~~~~~~~~ x_{1,2}=-2\pm\sqrt{3.85}$

в) Нули функции : решим уравнение при y = 0

$2(x+2)^2-6=0\\ (x+2)^2=3\\ x+2=\pm\sqrt{3}\\ x=-2\pm\sqrt{3}$

Функция убывает на промежутке x ∈ (-∞; -2), а возрастает - x ∈ (-2; +∞). Функция положительная при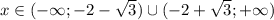 $x \in (-\infty;-2-\sqrt{3})\cup (-2+\sqrt{3};+\infty)$ , а отрицательная при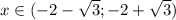 $x \in (-2-\sqrt{3};-2+\sqrt{3})$