под знаком корня записано число с 40 девятками после запятой корень √0.99...9 вычислите корень с 40 знаками после запятой

Ответы

Zsd19 16.09.2020 06:05

$\sqrt{\underbrace{99...9}_{40}}\approx 0.\underbrace{99...9}_{40}$

Пошаговое объяснение:

Дно число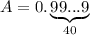 $A=0.\underbrace{99...9}_{40}$ . Требуется вычислить 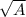$\sqrt{A}$ с 40 знаками после запятой.

$A=1-0.\underbrace{00...0}_{39}1=1-\dfrac{1}{10^{40}}$ 0<A<1Заметим, что если $0\leq x\leq 1$ , то $x\leq \sqrt{x}$ . И правда: рассмотрим $f(x)=\sqrt{x}-x,x\in [0;1]=f'(x)=\dfrac{1}{2\sqrt {x}}-1$ $\dfrac{1}{2\sqrt {x}}-1=0=2\sqrt {x}=1=\sqrt {x}=\dfrac{1}{2}=x=\dfrac{1}{4}$ . f'(x):

[0]+++++++++[1/4]------------[1] ; $f(0)=0;\;\;\;\;\;\;\;\;\;\;f(1)=0$ .А значит $f(x)\geq 0\;\forall x\in [0;1]$ А тогда $A\leq \sqrt{A}$ Также заметим, что $\sqrt{1-\dfrac{1}{10^{40}}}$ . И правда: $(1-\dfrac{1}{10^{41}})^2=1-\dfrac{2}{10^{41}}+\dfrac{1}{10^{82}}=1-\dfrac{1}{10^{40}}+(\dfrac{1}{10^{82}}+\dfrac{1}{10^{40}}-\dfrac{2}{10^{41}})=1-\dfrac{1}{10^{40}}+(\dfrac{1}{10^{82}}+\dfrac{8}{10^{41}})1-\dfrac{1}{10^{40}}$ А значит $A=0.\underbrace{99...9}_{40}\leq \sqrt{A}$ Т.к. 40 цифр после запятой в оценках слева и справа корня совпадают между собой, и равны 9, то и 40 цифр после запятой $\sqrt{A}$ равны 9. Целые части оценок равны 0, а значит и целая часть равна 0.А тогда $\sqrt{A}\approx 0.\underbrace{99...9}_{40}$