по мат анализу В задаче 7 вычислить определенный интеграл с
разложения подынтегральной функции в степенной ряд. Обеспечить
абсолютную погрешность
h =0,001

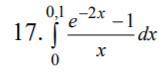
по мат анализу В задаче 7 вычислить определенный интеграл с разложения подынтегральной функции в ст

Ответы

кот929 27.04.2021 09:49

Пошаговое объяснение:

разложим эту страшную дробь в степенной ряд

сначала е⁻²ˣ -1, и поскольку нам нужно обеспечить абсолютную погрешность h =0,001, то возьмем первые четыре члена ряда

это будет

$\displaystyle e^{-2x}-1 = -1+\sum\limits_{k=0}^{4}\frac{(-2x)^k}{k!} =-2x+2x^2-\frac{4x^3}{3} +\frac{2x^4}{3}$

и тогда дробь наша разлагается в ряд

$\displaystyle \frac{e^{-2x}-1}{x} =-2+2x-\frac{4x^2}{3} +\frac{2x^3}{3}$

и тогда

$\displaystyle \int\limits^{0.1}_0 {(-2+2x-\frac{4x^2}{3} +\frac{2x^3}{3})} \, dx =$

$\displaystyle =-2x \bigg |_0^{0.1}+x^2\bigg |_0^{0.1}-\frac{4x^3}{9} \bigg |_0^{0.1}+\frac{x^4}{6} \bigg |_0^{0.1}-=$

здесь уже третий член ряда меньше требуемой точности 0,001, и поэтому если мы его отбросим

=-0.2 +0.01 =-0.190

ответ

$\displaystyle \int\limits^{0.1}_0 {\frac{e^{-2x}-1}{4} } \, dx \approx 0.19$ с точностью до 0,001

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

emilligrin 28.04.2019 13:48

Соочно нужно и пишите с решением...

шахноза31 28.04.2019 13:48

makskot69 28.04.2019 13:45

Вам 5. вычисли.38 + 2939 + 4833 + 5791 – 5485 - 3784 - 26...

КлименковЛеонид 28.04.2019 13:42

Lollimil 28.04.2019 13:40

Решить,,пример 4÷20/23+2 4/15×(2/7-4 11/14)...

дженни34 28.04.2019 13:38

ира1029 28.04.2019 13:34

dielela 28.04.2019 13:32

emkaemkovich902 28.04.2019 13:30

девочка261 28.04.2019 13:30