Вычислить объем тела, образованного вращениемвокруг оси оy фигуры, ограниченной графикамифункций . y = x^3 y=x^2
Другие вопросы по теме Математика
Популярные вопросы
- Корова -234ц пo26ц-?штТеленок-108ц по 12ц-?шт...
1 - ОҚЫЛЫМ ЖАЗЫЛЫМТапсырма. Тірек сөздерді пайдаланып, сұрақтарға жауап...
1 - Найдите моду и медиану числового ряда...
1 - Прихотливо извиваясь зимняя аллея устремляется за город снегири...
3 - АНГЛ.ЯЗ В 1 нужно найти ошибку Во 2 правильное поставить...
3 - ГОМОЛОГОМ АЦЕТИЛЕНА НЕ ЯВЛЯЮТСЯ 1)CH=C- CH2-CH3 4)CH=C -CH2-CH2-CH3...
3 - Народное собрание чем занимались...
1 - В тетрадь выписать основные формулы для повторения по темам: Свободное...
2 - 3 задание рассказ как друзья рыбу...
1 - Listen to Ian Marshall talking about his job as a lifeguard in...
3
ответ: π/12 единиц кубических.
Пошаговое объяснение:
Построим графики (рисунок 1).
Так как полученная фигура крутиться вокруг оси оу, выведем x из уравнений кривых:
Теперь найдём объём тела вращения. Делаем следующее:
1) Так как график![x=\sqrt[3]{y}](/tpl/images/0128/6284/27428.png) правее чем
правее чем 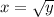 , то в интеграле отнимем правый график от левого графика.
, то в интеграле отнимем правый график от левого графика.
2) Так как график по оси оу находиться в диапазоне [0; 1], то и пределы интегрирования будут соответствующие.
3) По формуле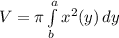 найдём объём, учитывая, что надо отнять правый график функции от левого.
найдём объём, учитывая, что надо отнять правый график функции от левого.
Эти шаги видно в рисунке 2.