Первой ткачихе требуется на выполнение половины заказа на 2 дня больше, чем первой для выполнения всего заказа. вместе они выполняют заказ на 1 день быстрее, чем выполняет вторая ткачиха. сколько дней необходимо каждой
ткачихи для выполнения заказа отдельно?

Ответы

Карычч 24.05.2020 01:29

Первой ткачихе требуется на выполнение половины заказа на 2 дня больше, чем ВТОРОЙ для выполнения всего заказа.

Пусть х дней требуется первой ткачихе на выполнение заказа, а второй - у дней. Тогда половину заказа первая ткачиха делает за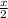 $\frac{x}{2}$ или у+2 дней. При совместной работе за 1 день они выполняют 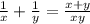$\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}$ , то есть весь заказ они выполнят за 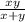$\frac{xy}{x+y}$ или у-1 день. Составим и решим систему уравнений:

$\left \{ {{\frac{x}{2}=y+2} \atop {\frac{xy}{x+y}=y-1}} \right.$

$\left \{ {{x=2y+4} \atop {\frac{(2y+4)y}{2y+4+y}=y-1}} \right.$

$\left \{ {{x=2y+4} \atop {\frac{2y^2+4y}{3y+4}=y-1}} \right.$

$\left \{ {{x=2y+4} \atop {2y^2+4y=3y^2+4y-3y-4}} \right.$

$\left \{ {{x=2y+4} \atop {3y^2+y-4-2y^2-4y=0}} \right.$

$\left \{ {{x=2y+4} \atop {y^2-3y-4=0}} \right.$

$\left \{ {{x=2y+4} \atop {y=4}} \right.$ $\left \{ {{x=2y+4} \atop {y=-1<0}} \right.$ (не подходит)

$\left \{ {{x=2\cdot4+4} \atop {y=4}} \right.$

$\left \{ {{x=12} \atop {y=4}} \right.$

ответ: для выполнения заказа в одиночку первой ткачихе требуется 12 дней, а второй - 4 дня.

ПОКАЗАТЬ ОТВЕТЫ

49583 10.01.2024 13:32

Пусть первая ткачиха нуждается в "х" днях для выполнения всего заказа. Тогда время, необходимое для выполнения половины заказа будет равно "х/2".

По условию задачи, первая ткачиха требует на выполнение половины заказа на 2 дня больше, чем на выполнение всего заказа. Таким образом, мы можем записать уравнение "х/2 = х + 2".

Что мы можем сделать с этим уравнением? Мы можем умножить его на 2, чтобы избавиться от дроби:

2 * (х/2) = 2 * (х + 2).
х = 2х + 4.

Теперь давайте решим это уравнение для "х":

х - 2х = 4.
-х = 4.
х = -4.

Итак, мы получили, что "х" равно -4. Так как время не может быть отрицательным, наше первоначальное предположение было неверным. Давайте попробуем другой подход.

Пусть первая ткачиха требует на выполнение всего заказа "у" днях. Тогда время, необходимое для выполнения половины заказа будет равно "у/2".

Мы также знаем, что вместе обе ткачихи выполняют заказ на 1 день быстрее, чем вторая ткачиха. Таким образом, время, необходимое для выполнения всего заказа первой ткачихой и второй ткачихой вместе, будет равно "у - 1".

Теперь у нас есть два уравнения, которые мы можем использовать для решения задачи:

у/2 = у - 1,
у = 2(у - 1).

Давайте решим эти уравнения:

у/2 = у - 1.
Перемножим оба уравнения на 2, чтобы избавиться от дроби:

2 * (у/2) = 2 * (у - 1),
у = 2у - 2.

Теперь вычтем "у" из обеих сторон:

у - 2у = -2,
-у = -2.

Итак, мы получили, что "у" равно 2. Теперь, когда у нас есть значение "у", мы можем найти время, необходимое каждой ткачихе для выполнения заказа отдельно.

Первая ткачиха нуждается в "у" днях, то есть 2 днях, для выполнения всего заказа.

Вторая ткачиха, судя по нашему второму уравнению, выполняет заказ на 1 день быстрее, чем обе ткачихи вместе, то есть $(у - 1)$ дней. Подставив значение "у" (2), мы получаем, что вторая ткачиха требует 1 день для выполнения заказа.

Итак, ответ на вопрос задачи заключается в следующем:
Первая ткачиха нуждается в 2 днях для выполнения всего заказа, а вторая ткачиха нуждается в 1 день.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика