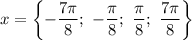ответить на теоретический вопрос и решить уравнение.

Другие вопросы по теме Математика
Популярные вопросы
- Нужно перевезти 1300т цемента по железной дороге.частью цемента...
1 - Сложные слова по 2 слова чтоб 2ой корень был такой -вар-вед -воз-вод-кол-коп-лов-мер-мет-ход...
3 - Написать мини сочинение по языку: wat your collection is : how you...
1 - Feso4+koh=feoh2+k+so4 (правельно написал? нигде индекс не забыл,поправте...
3 - Соблюдая нормы , составьте словосочетания со словами: 1.свойственный,...
2 - 1.напишите связный рассказ о герое романа дубровский дефорже. 2.в...
3 - Умоляю, ! (да я тупой, но только по ) отработка употребления past...
3 - Втигле находится расплавленный алюминий массой 3 кг при температуре...
2 - Уменя большая семья я ее люблю .как будет перевод на каз яз...
1 - Основания равнобедренной трапеции равны 14 и 6, один из углов равен...
1
Предел последовательности. Раскрытие неопределенности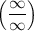 (с примером).
(с примером).
Число называется границей числовой последовательности
называется границей числовой последовательности 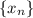 , если для любого
, если для любого 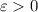 существует такой номер
существует такой номер 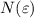 , что для всех
, что для всех 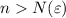 выполняется неравенство
выполняется неравенство 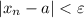
Символично это записывается так: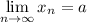 или
или  при
при 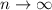
Для вычисления границ функций, заданных отношением двух многочленов в случае неопределенности типа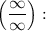
а) в числителе и знаменателе выносится в наивысшей степени. После соответствующих сокращений и, учитывая, что дроби типа
в наивысшей степени. После соответствующих сокращений и, учитывая, что дроби типа 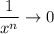 при
при 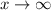 , получаем значение рассматриваемой границы;
, получаем значение рассматриваемой границы;
б) используются эквивалентные бесконечно большие, то есть
Тогда
При вычислении дробей, которые содержат иррациональность, выполняются аналогичные приемы.
Пример: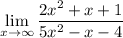
Решить уравнение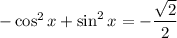 и отобрать его корни, принадлежащие промежутку
и отобрать его корни, принадлежащие промежутку ![[-\pi; \ \pi]](/tpl/images/1356/7292/6239f.png)
Отбираем корни, принадлежащие промежутку![[-\pi; \ \pi]:](/tpl/images/1356/7292/ed7a0.png)
Таким образом:
ответ: