Отрезок BD - биссектриса треугольника АВС. Найдите градусную меру угла CBD, если угол ABC = 67 градусов
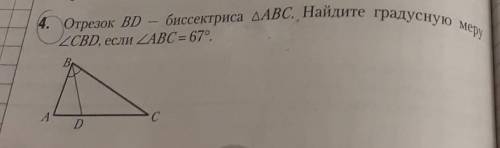
Другие вопросы по теме Математика
Популярные вопросы
- Nano3 + 2h = nano2 + h2o расставить степени окисления...
2 - Что хотели сказать авторы романом 12 стульев?...
1 - Решить уравнение: log(8)x+log(sqrt 2)x=14 ....
1 - 2. в объемом 25 л находится водород при температуре 300 к. после того как...
1 - Решить одну по .заранее . в стакан с соляной кислотой поместили кусочек...
3 - Длина плавательного бассейна 200м,ширина 50м.в бассейн налили 2000000л...
3 - На пагорбі гралося кілька мавп. третя частина мавп гралася біля підніжжя...
2 - Текст объёмом 1024 бита располагается в оперативной памяти, начиная с байта...
2 - Решить систему уравнений: 1) {4x-3y=12 {3x+4y=-24 2){ x-4y=-5 {x+y=5 3)...
1 - Сочинение по картине. свежий ветер.волга...
1
так как ВД биссектриса,то угол СВД =33,5
Согласно свойству биссектрисы, она делит противоположную сторону треугольника на отрезки, пропорциональные двум другим сторонам треугольника. В данном случае отрезок BD делит сторону AC на два отрезка AD и DC.
Теперь найдем соотношение между сторонами треугольника АВС. В треугольнике АВС у нас есть известный угол ABC, который равен 67 градусов.
Так как угол ABC является вертикальным углом для другого угла у треугольника, то угол ACB также равен 67 градусов.
Теперь мы можем использовать свойство биссектрисы. Поскольку BD делит сторону AC на отрезки, пропорциональные сторонам AB и BC, мы можем записать соотношение:
AD/DB = AC/CB
Так как мы знаем, что угол ABC равен 67 градусам, мы можем записать:
AD/DB = AC/CB = AB/BC
Теперь мы можем использовать эту пропорцию, чтобы найти соотношение между AD и DB.
AD/DB = AB/BC
Подставим известные значения:
AD/DB = AB/BC = AB/AD
Упростим выражение:
AD^2 = AB * DB
Теперь у нас есть соотношение между AD и DB, которое можно использовать для нахождения градусной меры угла CBD.
Обратимся к изначальному треугольнику АВС. У нас уже есть известное значение угла ABC, который равен 67 градусам.
Используя свойство треугольника, сумма углов треугольника равна 180 градусов, мы можем записать:
ACB + ABC + BAC = 180
67 + BAC + BAC = 180
2BAC = 180 - 67
2BAC = 113
BAC = 113 / 2
BAC = 56.5
Таким образом, градусная мера угла BAC равна 56.5 градусам.
Снова обратимся к соотношению:
AD^2 = AB * DB
Так как мы знаем, что угол BAC равен 56.5 градусам, мы можем заменить AB и DB значениями сторон треугольника:
AD^2 = 56.5 * 56.5
AD^2 = 3192.25
AD = √3192.25
AD ≈ 56.5
Теперь мы знаем значение AD, и мы также помним, что BD делит сторону AC на два отрезка AD и DC.
Поскольку AD ≈ 56.5, то DC ≈ 56.5.
Теперь мы можем найти градусную меру угла CBD, используя соотношение:
AD/DB = AC/CB
56.5/DB = 113/CB
CB = DB * (113/56.5)
CB = 2 * DB
То есть, градусная мера угла CBD равна удвоенной градусной мере угла DBA.
Таким образом, градусная мера угла CBD равна 2 * DBA.
Обратимся к треугольнику ABD. У нас уже есть выражение для AD:
AD ≈ 56.5
DBA + BDA = 180
DBA + 67 = 180
DBA = 180 - 67
DBA = 113
Итак, градусная мера угла DBA равна 113 градусам.
Теперь мы можем найти градусную меру угла CBD, удвоив градусную меру угла DBA:
CBD = 2 * DBA
CBD = 2 * 113
CBD = 226
Таким образом, градусная мера угла CBD равна 226 градусам.
Ответ: Градусная мера угла CBD равна 226 градусам.