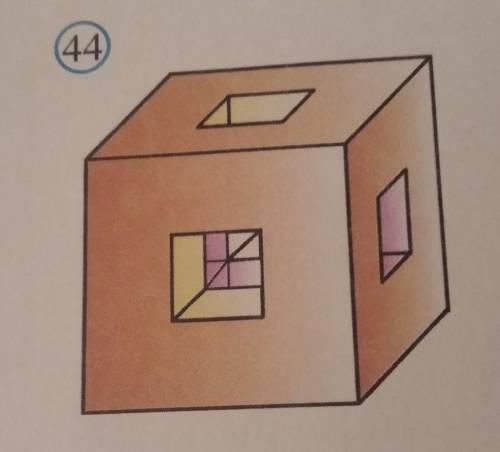
Основание поперечного сечения куба с ребром равным 3 см. пересекающее все его рёбра, - вырезает квадратные отверстия со стороной 1 см. (рис. 44). Найдите площадь полной поверхности оставшейся части куба с полным решением​

Добрый день! Давайте рассмотрим эту задачу вместе. Дано, что основание поперечного сечения куба вырезает квадратные отверстия со стороной 1 см. Для начала, давайте разберемся, какие данные у нас есть и что нам нужно найти. У нас есть: - ребро куба, которое равно 3 см Нам нужно найти: - площадь полной поверхности оставшейся части куба Чтобы решить эту задачу, мы должны найти площадь каждой из плоскостей, которые были вырезаны, а затем вычесть эти площади из общей площади куба. 1. Площадь каждой вырезанной плоскости: На рисунке видно, что каждая вырезанная плоскость - это квадрат со стороной 1 см. Обратите внимание, что куб имеет 6 таких плоскостей - 1 на каждой стороне. Таким образом, площадь каждой вырезанной плоскости равна 1 см * 1 см = 1 кв.см. 2. Общая площадь всех вырезанных плоскостей: Так как у нас есть 6 вырезанных плоскостей и каждая из них имеет площадь 1 кв.см, общая площадь всех вырезанных плоскостей равна 6 * 1 кв.см = 6 кв.см. 3. Общая площадь оставшейся части куба: Для того чтобы найти общую площадь оставшейся части куба, мы должны вычесть площадь всех вырезанных плоскостей из общей поверхности куба. Площадь общей поверхности куба вычисляется по формуле: 6 * (сторона куба)^2. В данном случае сторона куба равна 3 см, поэтому площадь общей поверхности куба равна 6 * (3 см)^2 = 6 * 9 кв.см = 54 кв.см. Теперь вычтем площадь всех вырезанных плоскостей из общей площади куба: Общая площадь оставшейся части куба = 54 кв.см - 6 кв.см = 48 кв.см. Таким образом, площадь полной поверхности оставшейся части куба равна 48 кв.см. Надеюсь, что мое объяснение было понятным и подробным. Если у вас остались какие-либо вопросы, пожалуйста, задайте их.