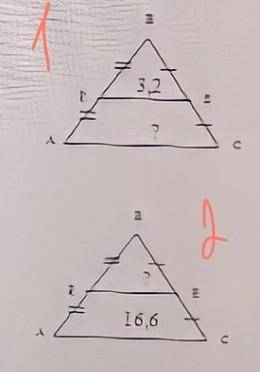
очень в треугольнике ABC найдите AВС, если PE = 3,2. АС =.
2. в треугольнике АВС, найдите PE, если АС = 16,6 см. PE = .
3. периметр равностороннего треугольника равен 18 см. Найдите длину средней линии треугольника:
а) 4см, б) 9 см, в) 6 см, г) 3 см.

1. Для того чтобы найти значение угла АВС в треугольнике ABC, нам необходимо знать соотношение длин сторон треугольника. Основываясь на изображении треугольника ABC, мы видим, что сторона AB параллельна стороне PC, поэтому угол АВС равен углу PCE. Из условия задачи дано, что PE = 3.2. Также, поскольку треугольник ABC - прямоугольный, со сторонами AC и AB являются катетами, мы можем использовать теорему Пифагора для нахождения длины стороны BC:

BC^2 = AB^2 + AC^2

Так как сторона AB равна PE (3.2), а сторона AC равна 2, мы можем подставить эти значения в уравнение:

BC^2 = (3.2)^2 + 2^2
BC^2 = 10.24 + 4
BC^2 = 14.24
BC ≈ √14.24
BC ≈ 3.77 (округляя до двух десятичных знаков)

Теперь, чтобы найти значение угла AВС, мы можем использовать тангенс угла PCE:

tan(AВС) = PE / BC
tan(AВС) = 3.2 / 3.77
tan(AВС) ≈ 0.849
АВС ≈ arctan(0.849)
АВС ≈ 40.12 градусов (округляя до двух десятичных знаков)

Таким образом, угол АВС в треугольнике ABC примерно равен 40.12 градусов.

2. Для нахождения значения PE в треугольнике АВС, нам необходимо знать размеры других сторон треугольника. Однако, в условии задачи дано только значение стороны АС, которая равна 16.6 см. Мы не можем определить значение PE без этой информации.

3. Для нахождения длины средней линии треугольника, нам необходимо знать его периметр. В условии задачи сказано, что периметр равностороннего треугольника равен 18 см. Зная, что равносторонний треугольник имеет все три стороны одинаковой длины, мы можем поделить периметр на 3 для нахождения длины одной стороны:

Длина одной стороны = Периметр / 3
Длина одной стороны = 18 / 3
Длина одной стороны = 6 см

Теперь, чтобы найти длину средней линии треугольника, мы можем использовать формулу:

Длина средней линии = (Длина одной стороны) / 2
Длина средней линии = 6 / 2
Длина средней линии = 3 см

Таким образом, если периметр равностороннего треугольника равен 18 см, то длина средней линии составляет 3 см.