Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 30 градусов. найдите объем конуса

Ответы

Диарочка1 03.10.2020 18:41

Рисунок прикреплен.

Дано: конус, ВС=12 см, ∠НСВ=30°

Найти: объем конуса

Решение: по условию образующая конуса наклонена к плоскости под углом в 30°. Это значит, что угол между образующей и радиусом основания конуса 30°.

Из вершины конуса опустим высоту. Обозначим её ВН.

ΔВНС прямоугольный.

У него известна гипотенуза ВС=12 и ∠НСВ=30°.

В прямоугольном треугольнике катет, лежащий напротив угла в 30° в два раза меньше гипотенузы.

$BH=\frac{BC}{2}=\frac{12}{2}=6$

По теореме Пифагора найдем второй катет ΔВНС. Он же является радиусом основания конуса.

$HC=\sqrt{BC^2-BH^2}=\sqrt{12^2-6^2}=\sqrt{144-36}=\sqrt{108}$

Объем конуса вычисляется по формуле: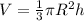 $V=\frac{1}{3}\pi R^2h$ , где R - радиус основания, h - высота конуса.

$V=\frac{1}{3}\pi R^2h=\frac{1}{3}\pi (\sqrt{108})^2*6 =108*2\pi =216\pi$

ответ: 216π см³

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

ника2092 12.06.2019 12:00

dĵdjdkdkdkdkdk 12.06.2019 12:00

Округлите число 8999996 до разряда миллиона...

oliaborisova123 12.06.2019 12:00

ник4760 12.06.2019 12:00

Кэт32131 12.06.2019 11:50

юлиядзудзе 12.06.2019 11:50

Retyyyghiop 12.06.2019 11:50

АружанТопская 12.06.2019 11:50

Alinaakconova9 12.06.2019 11:50

mschibarova201 12.06.2019 11:50

4*61x-464=1000 решительно уровнение...