Обчислити площу фігури, обмежену лініями: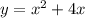 , y=x+4.
, y=x+4.
Другие вопросы по теме Математика
Популярные вопросы
- Мороз. снег украл в каком из выделенных слов все согласные звуки- парные...
1 - Что означает слово кило в словах километр, килограмм...
1 - Среднее арифметарифметичеткое число n и m равно20.найдите эти числа,...
3 - Маша сказала а не вчера бабушка отметила свой 16 день рождения. аня...
1 - Решите дроби напишите как вы их решили 3/50+18/25= 43/62-10/31= 29/64+3/8=...
1 - Сколько двузначных чисел сумма цифр которых равна нечетному числу можно...
3 - Каким понятием можно назвать группу людей, говорящий на одном языке,...
1 - Запиши двузначные числа, при умножении единиц которых на 3 применяется...
1 - На склад 2ц 5 кг картофеля , 1 ц 65 кг моркови и 85 кг лука . сколько...
2 - Он взял большущую тетрадь,задкмчиво погрыз карандаш,почесал ухо,попил...
3
Пошаговое объяснение:
рисуем графики, определяем фигуру и пределы интегрирования
и получаем