Найти y’
в) y=lnx/x^3+1
г)y=(Корень из x +1)e^x
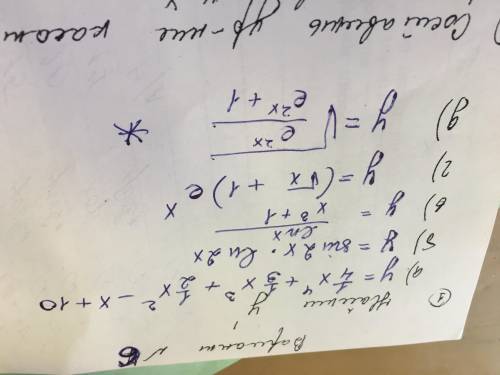
Другие вопросы по теме Математика
Популярные вопросы
- Даны координаты вершин треугольника abc.. a(1; 3; 0) b(3; 0; 4)...
2 - Завтра кр. по ! если вероятность попадания в мишень 0,6 тогда...
2 - Где капли запасного масла в клетках семян масличных растений:...
2 - Краткое содержание сказок льва толстого акула прыжок птичка лев...
2 - Найдите x из пропорции: 3: (5/8x)=1 2/9: 4 2/3...
2 - You spent a week visiting your friend sam in scotland. write a...
1 - Как провести опыт: осуществление превращения: соль- нерастворимое...
2 - Два слесаря работая вместе могут выполнить на 8 дней быстрее,...
1 - Найдите в интернете примеры писем официально-делового стиля ....
3 - Какое вещество ch3-ch2-c-h. || ch-ch3...
3
Пошаговое объяснение: