Найти все значения параметра к
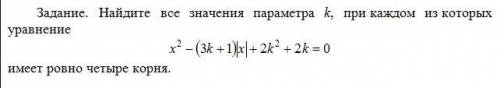
Другие вопросы по теме Математика
Популярные вопросы
- О колеблющегося на ветру флаге, падающего кленового листка,пахнувшим...
3 - Решите пунктуационные задачи в сложносочинённых предложениях....
2 - Прочитайте 1-3 главы повести Тарас Бульба , составьте пять хороших,...
2 - решить задачи по географии 2) Визначте місцевий час у пункті...
3 - Решите иррациональную систему уравнений...
3 - Укажите варианты ответов, в которых во всех словах одного ряда...
2 - Найдите по формуле пути s=vt значение s, если: а) v=9 1/2 км/ч,...
3 - По плану этому написать сочинение по картине Яблонского Утро...
3 - Согласно ЗСМ : масса... веществ равна массе ... реакции...
1 - надо написать сочинение до 12:00. Написать сочинение на тему...
3
k∈(-∞;1)∪(1;+∞)
Пошаговое объяснение:
Раскрываем модуль по определению:
Уравнение имеет 2 решения, если дискриминант >0
D=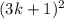 -4(2k²+2k)>0
-4(2k²+2k)>0
9k²+6k+1-8k²-8k>0
k²-2k+1>0
(k-1)²>0
Это парабола, ветви направлены вверх и она всегда положительна на всей оси Ох, только в точке k=1 принимает значения 0, значит k принимает все значения, кроме 1
аналогично для второго уравнения, тот же дискриминант и >0
ответ: k∈(-∞;1)∪(1;+∞)