Найти все натуральные числа а и в такие что а^2 +b и b^2+a - квадраты

Ответы

vlad369cool 15.10.2020 16:35

ответ: нет таких натуральных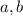 a,b

Пошаговое объяснение:

$b^2+ab^2\\a^2+ba^2$

Поскольку числа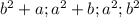 b^2+a;a^2+b;a^2;b^2 полные квадраты, а числа 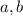a,b натуральные, то

$b^2+a\geq (b+1)^2\\b^2+a\geq b^2+2b+1\\a\geq2b+1 \\a^2+b\geq(a+1)^2\\a^2+b\geq a^2+2a+1\\b\geq2a+1\\\left \{ {{a\geq 2b+1} \atop {b\geq 2a+1}} \right.$

Сложим полученные неравенства почленно:

$a+b\geq 2a+2b+2\\a+b\leq -2$

Что невозможно для натуральных чисел и .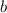

Как видим, таких натуральных и 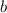не существует.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

nastenkastetsen 24.03.2019 16:48

Каково наименьшее число учеников класса, где доля мальчиков равна 55%?...

EgorUmelii 24.03.2019 16:48

Среди 8 монет есть десятирублёвые. сколько среди них десятирублёвых монет, если среди любых пяти монет, по крайней мере, три монеты одинакового достоинства, но нет пяти монет...

lenalorax9093 24.03.2019 16:48

Вшкольном саду 3ряла кустов смородины,по 5кустов в каждом ряду сколько всего кустов смородины в школьном саду?...

ДлЯсВоИхПро100АлЯ 24.03.2019 16:49

Объясни что показывает каждое выражение составленное по следующей таблицы...

Saens321 24.03.2019 16:49

Выражения а и в, затем найти частное а: в и произведение а*в а= 2/ х-4 -2х+6/ х²-16= в=х+4/2х-8 +8х/16-х²= а: в= а*в= 3) а=3/х+1 -6/х= в=2/х +2х-8/х²+2х= а: в= а*в=...

olga877 24.03.2019 16:50

Прямоугольный лист бумаги размерами 19 см×31 см согнули вдоль некоторой прямой, пересекающей противоположные края листа. площадь полученной фигуры может быть равна … а. 294...

Nikitosqwerty 24.03.2019 16:52

Длина прямоугольного паралипипеда равна 18 см,ширина в 2 раза меньше длины, а высота-на 11 см больше ширины. вычислите объем паралипипеда...

temirlan2019p 24.03.2019 16:53

Даны два треугольника с одинаковым периметром: один равнобедренный и один равносторонний треугольник. основание равнобедренного треугольника составляет 15 см, а боковой край...

danilaokolot 24.03.2019 17:01

Решить варианты под номером 6. заранее )...

Anna14124 24.03.2019 17:02

Грани куба размерами 4 см×4 см×4 см красные и синие, причём у любой пары противоположных граней цвета разные. куб разрезали на кубики с ребром 1 см. сколько среди них будет...

Найти все натуральные числа а и в такие что а^2 +b и b^2+a - квадраты

Популярные вопросы