Найти вероятность того что при 180 бросании игральной кости число 6 выпадет менее 28 раз
Ответы
Рассматриваем схему испытаний Бернулли (число испытаний n-180) с вероятностью успеха p= 1/6 (вероятность выпадания числа 6). Успехом считаем выпадание числа 6. Матожидание числа успехов М=n*p=180*1/6=30. Дисперсия D=n*p*(1-p)=30*(1-1/6)=25. Обосначим mu=28, теперь P(mu<28)=P((mu-M)/(√D))≥(mu-n*p)/√(n*p*(1-p))=P(((mu-M)/(√D))≥(28-30)/√25)=1/√6.28*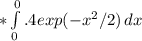 , dx=0.5-0.15542=0.345.
, dx=0.5-0.15542=0.345.
ПОКАЗАТЬ ОТВЕТЫ
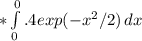 , dx=0.5-0.15542=0.345.
, dx=0.5-0.15542=0.345.
Другие вопросы по теме Математика
Популярные вопросы
- Какое количество вещества водорода содержится в 2,94г гидроксида меди(ii)?...
2 - Составьте уравнения реакций сообщение между простыми веществами при которых...
1 - При подъёме ящика с гвоздями на высоту 5 м, выполнена работа в 1582 дж....
2 - Составьте предложения подчеркните грамматическую основу и укажите чем они...
1 - Морфологический разбор слова рвётся...
1 - Длина прямоугольного параллелепипеда равна 8 см высота 4 см а площадь его...
1 - Write sentences that show different opinions about music. draw a table of...
2 - Червячков. в этом слове буква я к какой орфограмме относится ( сразу говорю...
3 - Из двух станций одновременно вышли навстречу друг другу два поезда. через...
3 - Москва-центр борьбы с ордынским владычеством. куликовская битва. напишите...
2