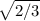Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R
Знаю только то что в решении используются производные ...

Радиус основания = R*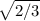, высота = R * 2/.

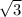Пошаговое объяснение:

Посмотрим на шар сбоку (см. рис). Тогда цилиндр мы будем видеть как прямоугольник. Пусть, a - диаметр круга в основании цилиндра, b - высота цилиндра. Тогда объем цилиндра вычисляется по формуле

V = pi * (a/2)² * b = (pi/4) * a²b

Чтобы объем был максимальным, нужно, чтобы величина a²b была максимальной. Заметим, что a² = c²-b² = 4R² - b²

max(a²b) = max((4R²-b²)*b)

Пусть, f(b) = (k-b²)*b, где k = 4R².

Эта функция имеет график, как на рисунке, т.е. проходит через точку (0;0). Нас интересует максимум при b>0. Он достигается в точке, где f'(b) = 0.

f'(b) = k - 3b² = 0.

b = +-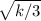

b = -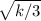 не подходит, т.к. b положительно.

Значит, b =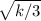 = R * 2/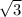

a =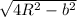 = = 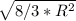R * 2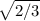, радиус основания в 2 раза меньше, т.е. R*