Найти первообразную f(x) = 6 cos (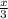 ) + 1.
) + 1.
Другие вопросы по теме Математика
Популярные вопросы
- Дополните предложения однордными членами.запишите 1)яблоки .2)в каспийском...
2 - Как у наших у ворот за горою жил да был бутерброд с колбасою.захотелось...
2 - Строительство детского сада обошлось в двести пятьдесят тысяч манат...
2 - Решите уравнение: (x+4/21)-4/15=16/35...
2 - Порядковый номер атома натрия равен:...
3 - Оно освежит своими потоками землю и жизнь будет продолжаться дальше....
1 - 100 ! выпишите из предложения устаревшее словосочетание и подберете...
3 - Корень из 53. разложить на множители...
1 - Примеры 1)378200: 1525=? 2)238119: 1173=?...
1 - Монолог рассуждение по пословице пустые слова, что орех без ядра...
3
F ( x ) = 18 sin ( 1 /3 x ) + x + C
Пошаговое объяснение:
Функция F ( x ) может быть найдена с вычисления неопределенного интеграла от производной f ( x ) .
F ( x ) = ∫ f ( x ) d x
Выпишем интеграл, чтобы решить его.
F ( x ) = ∫ 6 cos ( x/ 3 ) + 1 d x
Разложим интеграл на несколько интегралов.
∫ 6 cos ( x /3 ) d x + ∫ 1 d x
Поскольку 6 является константой по отношению к x , вынесем 6 из интеграла.
6 ∫ cos ( x /3 ) d x + ∫ 1 d x
Пусть u = x 3 . Тогда d u = 1 3 d x , следовательно 3 d u = d x . Переписать, используя u и d u .
6 ∫ cos ( u ) 1 /(1/ 3) d u + ∫ 1 d x
Упростим.
6 ∫ 3 cos ( u ) d u + ∫ 1 d x
Поскольку 3 является константой по отношению к u , вынесем 3
из интеграла.
6 ( 3 ∫ cos ( u ) d u ) + ∫ 1 d x
Умножим 3 на 6 .
18 ∫ cos ( u ) d u + ∫ 1 d x
Интеграл cos ( u ) относительно u равен sin ( u ) .
18 ( sin ( u ) + C ) + ∫ 1 d x
Поскольку 1 является константой по отношению к x , вынесем 1 из интеграла.
18 ( sin ( u ) + C ) + x + C
Упростим.
18 sin ( u ) + x + C
Заменим все u на x /3 .
18 sin ( x /3 ) + x + C
Изменим порядок членов и получаем ответ:
F ( x ) =18 sin ( 1 /3 x ) + x + C