найти неопределенный интеграл
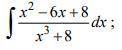
Другие вопросы по теме Математика
Популярные вопросы
- 4. разгадайте кроссворд по теме «здоровье и забота о нём»: across: 1. a place...
3 - 5. распределите предложения по двум столбикам «bad habits» и «good habits»:...
1 - Знайти площу ромба якщо його тупий кут дорівнює 120 градусів . а менша діагональ...
2 - Обчисліть масові частки елементів у глюкозі...
2 - Какие есть цитаты известных поэтов про дон кихота...
2 - На нити, перекинутой через блок, подвешены грузы массами по 500 г. какой груз...
1 - Найдите коэффициент полезного действия примуса, в котором при нагревании воды...
2 - Уяви собі що ти репортер місцевої газети радіо чи телебачення а твій друг спротсмен....
2 - Какой из перечисленных треугольников построить невозможно? а) треугольник со...
1 - Два десантника гаврила и ермила выпрыгнули из самолета на высоте 10 км и летят...
2
С неопределенных коэффициентов: