Найти координаты вектора y=A ̃(x), если оператор A ̃ задан матрицей А и дан вектор x: 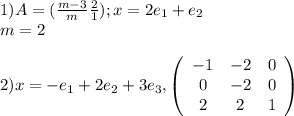
Другие вопросы по теме Математика
Популярные вопросы
- Как переводятся предложения it s ten to six...
3 - Какова величина равнодействующей силы (кн) , которая действует на поезд массой...
3 - )) переведите на язык, обращая внимание на причастия. определите тип причастия....
3 - Какие происшествия в жизни земли связанны с космическими явлениями?...
3 - Рассказ л.пантелеева. новенькая когда происходили события?...
2 - Варифметичній прогресії (аn), a2=-4, a4=2. знайдіть а6....
1 - Стили речи, предложенные ф.м.ломоносовым | жанр | высокий стиль | средний...
1 - Разобрать слова по составу : грунтобетонный безвластие бездельничать...
1 - Велектричному колі прилади ідеальні.потужність лампи 20 вт,вокази вольтметра...
2 - Как составить из трёх цифр 3 число 11 и за .....
3
Дано:
A = \(\begin{pmatrix} -1 & -2 & 0 \\ 0 & -2 & 0 \\ 2 & 2 & 1 \end{pmatrix}\)
x = -e1 + 2e2 + 3e3
Необходимо вычислить:
y = Ã(x)
Шаг 1: Выразим вектор x в виде матричного произведения
x = -e1 + 2e2 + 3e3 = \(\begin{pmatrix} -1 \\ 2 \\ 3 \end{pmatrix}\)
Шаг 2: Вычислим матрицу-векторное произведение
y = Ã(x) = A * x
y = \(\begin{pmatrix} -1 & -2 & 0 \\ 0 & -2 & 0 \\ 2 & 2 & 1 \end{pmatrix}\) * \(\begin{pmatrix} -1 \\ 2 \\ 3 \end{pmatrix}\)
Шаг 3: Выполним умножение матрицы на вектор
y = \(\begin{pmatrix} (-1 * -1) + (-2 * 2) + (0 * 3) \\ (0 * -1) + (-2 * 2) + (0 * 3) \\ (2 * -1) + (2 * 2) + (1 * 3) \end{pmatrix}\)
y = \(\begin{pmatrix} 1 + (-4) + 0 \\ 0 + (-4) + 0 \\ (-2) + 4 + 3 \end{pmatrix}\)
y = \(\begin{pmatrix} -3 \\ -4 \\ 5 \end{pmatrix}\)
Ответ: Координаты вектора y = Ã(x) равны (-3, -4, 5).