Найти интеграл от выражений, содержащих квадратный трехчлен. ( Если можно без лишнего)
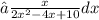
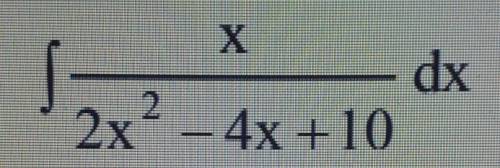
Другие вопросы по теме Математика
Популярные вопросы
- Задание 1. Bilde die Fragen und antworte darauf. Образуй вопросы (здесь...
1 - Определите КПД атомной электростанции, если в минуту в ее реакторах сжигается...
3 - Как называлась песня я сделаю вдох так пахнет Диор я искал тебя вечно...
1 - Любой рождественский рассказ краткого содержания без разницы Любой но...
2 - С встречных вопросов проверьте знания своеготоварища поправиламбезопасностиобращения...
1 - Обоснуйтенеобходимостьтренировки вразборке и сборкеавтомата...
1 - Как называется песня в которой поётся в камине в 6 утра ? ...
3 - Вычислите массу углекислого газа,если сгорело 200 граммов угля(углерода)....
1 - Які фактори викликали мілгтаризацію японської економіки та посилення впливу...
1 - Доведіть або спростуйте тезу: «Культура Русі-України формувалася внаслі...
2
Делаем в числителе производную знаменателя:
В первом интеграле 4х-4 заносим в дифференциал, во втором выделяем в знаменателе квадрат разности