Найти dx(a)/dl если я= (2x-1)y^2+ y/x l(3; 4) a(1; 2)
Ответы
Производная функции z по направленю 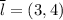 в точке А(1,2).
в точке А(1,2).
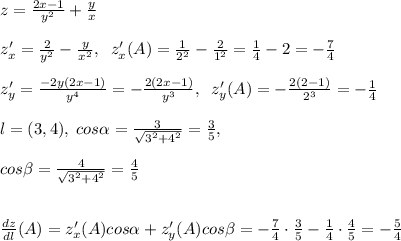
ПОКАЗАТЬ ОТВЕТЫ
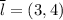 в точке А(1,2).
в точке А(1,2).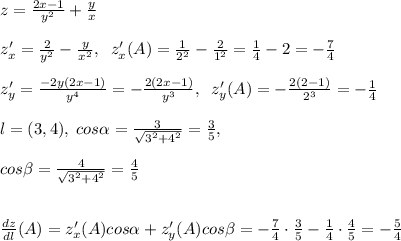
Другие вопросы по теме Математика
Популярные вопросы
- Почему «смешная» повесть завершается словами автора: «Скучно на этом свете,...
1 - Какие странности и неожиданности в поведении разных персонажей повести...
1 - Перечитайте характеристику героев и определите, в чём её необычность,...
2 - От чьего имени написано «Завещание» и почему? Какое впечатление создаётся...
2 - Почему обретённая свобода не принесла герою счастья? Пушкин Цыганы...
2 - Согласны ли вы с суждением критика В. Г. Белинского о «Завещании»: в нём...
2 - Какое стихотворение А. С. Пушкина вспомнилось по ассоциации с «Молитвой»...
2 - Объясните, почему так много многоточий в тексте стихотворения. - Лермонтов...
2 - С каких приёмов поэту удаётся открыть вам внутренний мир человека? - Лермонтов...
1 - Свобода и покой равнозначны счастью или противостоят ему? (Вспомните,...
3