1. Математика
  2. Найти частное решение дифференциального

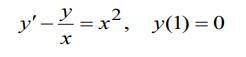
Найти частное решение дифференциального уравнения, удовлетворяющее
заданным начальным условиям:


Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям:

KarinkaChernov KarinkaChernov    3   05.11.2020 14:05    0

Ответы
Thanks2y Thanks2y  05.12.2020 14:06

y - \frac{y}{x} = x {}^{2}

Возьмите производную

\frac{d}{dy} (y) - \frac{d}{dy}( \frac{y}{x} ) \frac{d}{dy} (x {}^{2} )

Дефферицировать

Использовать правила дефферицирования

1 - \frac{ \frac{d}{dy}(y) \times x - y \times \frac{d}{dy} (x) }{x {}^{2} } = \frac{d}{dx} (x {}^{2} ) \times \frac{dx}{dy}

Упростить

Деференцировать

1 - \frac{x - y \times 1 \times \frac{dx}{dy} }{x {}^{2} } = 2x \times \frac{dx}{dy}

Вычеслите произведение

1 - \frac{x - y \times \frac{dx}{dy} }{x {}^{2}} = 2x \times \frac{dx}{dy}

Умножить обе части

x {}^{2} - (x - y \times \frac{dx}{dy} ) = 2x {}^{3} \times \frac{dx}{dy}

Раскрыть скобки

x {}^{2} - x - y \times \frac{dx}{dy} = 2x {}^{3} \times \frac{dx}{dy}

Перенесите слагаемые в др часть уравнения

y \times \frac{dx}{dy} - 2x {}^{3} \times \frac{dx}{dy} = x {}^{2} + x

Разложите выражение на множители

(y - 2x {}^{3} ) \times \frac{dx}{dy} = - x {}^{2} + x

Разделите обе стороны

\frac{dx}{dy} = \frac{ - x {}^{2} + x }{y - 2x {}^{3} }

2) у=0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
nikasimonok2007 nikasimonok2007  03.03.2021 10:05
Математика, 6 класс, 3 четверть...
никитос73803 никитос73803  03.03.2021 10:05
Скорость велосипеда 12,3 км/ч. Какое расстояние проедет велосипедист за 4ч 12мин?​...
zhelavskaitanya zhelavskaitanya  03.03.2021 10:05
Сравни дроби 3/140 или же 2/140​...
shams200108 shams200108  03.03.2021 10:04
ЗАДАЧА 4 Поділіть даний відрізок навпіл.РОЗВ ЯЗАННЯ. Нехай AB даний відрізок(мал. 244). З точок AiB радіусом AB описуемо дути.Вони перетнуться в деяких точках С1 D.Пряма...
ibatulina03 ibatulina03  03.03.2021 10:03
Задание 4 Запиши смешанное число в виде неправильной дроби: 6/9Запиши неправильную дробь в виде смешанного числа:18/8​...
lokosso lokosso  03.03.2021 10:03
10 целых - 5/7= __целых_/_...
MashaTears1 MashaTears1  03.03.2021 10:03
вычислить действиями столбиком ​...
КристинаСоболева КристинаСоболева  03.03.2021 10:02
Помагите решить у миня сор на всех потпншусь и паставлю по балу​...
HELPERSKINE HELPERSKINE  03.03.2021 10:01
Выдели глаголы настоящего и будущего времени во втором лице единственного числа человек не ценит твои за тех пор пока не иссякнет источник но жители пустыни в хорошо знает...
ЛизаНагайцева03 ЛизаНагайцева03  03.03.2021 10:01
4 . В координатной плоскости отметьте точки А(– 5; –2), В(–2; 1), С(1; 1) Найдите: а) координаты точки пересечения отрезка АВ с осью абсцисс; b) координаты точки пересечения...

Популярные вопросы