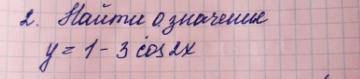
Другие вопросы по теме Математика
Поворозник
27.03.2022 03:54
Стефанія2016
27.03.2022 04:00
свитек
27.03.2022 04:22
VarmaleyYouTuber
27.03.2022 04:42
choika64
27.03.2022 04:42
Nagoshka
27.03.2022 04:59
zhienalinaadel
27.03.2022 05:04
Ronaldinho2003
27.03.2022 05:29
Rabika2018
27.03.2022 05:30
Популярные вопросы
- 1.Напишіть 4 тези до питання Становище Німеччини після Другої світової...
1 - На какой во отвечает проблема произведения? Подскажите...
3 - Як ви вважаєте, що означає поняття духовний вибір людинт в житті ?...
3 - Найти эпизоды в первой части романа «Преступления и Наказания», как...
2 - Скласти формули речовин етилацетату...
2 - Не виконуючи побудов знайти координати точок перетину графіка функції...
2 - Перечислите природные зоны Евразии с запада на восток по 50 - ой параллели...
2 - State the type of voice in the sentences. (Определи тип залога в следующих...
3 - В арифметической прогрессии А1=-10, а5=-4. Найдите сумму первых 8 членов...
3 - Переведите из прямой речи в косвенную ....
3
ответ: Перепишем выражение в виде
−
3
cos
(
2
x
)
+
1
.
−
3
cos
(
2
x
)
+
1
Используем вид записи
a
cos
(
b
x
−
c
)
+
d
для поиска переменных, используемых для вычисления амплитуды, периода, сдвига по фазе и вертикального сдвига.
a
=
−
3
b
=
2
c
=
0
d
=
1
Найдем амплитуду
|
a
|
.
Амплитуда:
3
Определим период при формулы
2
π
|
b
|
.
Нажмите, чтобы отобразить меньше шагов...
Период функции можно вычислить с
2
π
|
b
|
.
Период:
2
π
|
b
|
Подставим
2
вместо
b
в формуле для периода.
Период:
2
π
|
2
|
Решим уравнение.
Нажмите, чтобы увидеть больше шагов...
Период:
π
Найдем сдвиг периода при формулы
c
b
.
Нажмите, чтобы отобразить меньше шагов...
Фазовый сдвиг функции можно вычислить с
c
b
.
Фазовый сдвиг:
c
b
Заменим величины
c
и
b
в уравнении для фазового сдвига.
Фазовый сдвиг:
0
2
Делим
0
на
2
.
Фазовый сдвиг:
0
Найдем вертикальное смещение
d
.
Вертикальный сдвиг:
1
Перечислим свойства тригонометрической функции.
Амплитуда:
3
Период:
π
Фазовый сдвиг:
0
(на
0
вправо)
Вертикальный сдвиг:
1
Выберем несколько точек для нанесения на график.
Нажмите, чтобы отобразить меньше шагов...
Найдем точку при
x
=
0
.
Нажмите, чтобы увидеть больше шагов...
−
2
Найдем точку при
x
=
π
4
.
Нажмите, чтобы увидеть больше шагов...
1
Найдем точку при
x
=
π
2
.
Нажмите, чтобы увидеть больше шагов...
4
Найдем точку при
x
=
3
π
4
.
Нажмите, чтобы увидеть больше шагов...
1
Найдем точку при
x
=
π
.
Нажмите, чтобы увидеть больше шагов...
−
2
Перечислим точки в таблице.
x
f
(
x
)
0
−
2
π
4
1
π
2
4
3
π
4
1
π
−
2
Тригонометрическую функцию можно изобразить на графике, опираясь на амплитуду, период, фазовый сдвиг, вертикальный сдвиг и точки.
Амплитуда:
3
Период:
π
Фазовый сдвиг:
0
(на
0
вправо)
Вертикальный сдвиг:
1
x
f
(
x
)
0
−
2
π
4
1
π
2
4
3
π
4
1
π
−
2