Найти производную y=f(x)
фото прикрепил
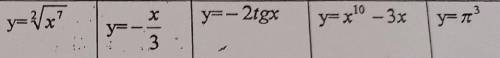
Другие вопросы по теме Математика
Популярные вопросы
- Реши уравнение: −5x−16=5x+34. ответ: x=...
2 - Назовите предков Касым хана 2)где находилась территория казахского...
3 - какое число надо подставить вместо x чтобы в выражении (x^4)(2x^2+3x-1)(x^2+mx-3)...
2 - Площадь поверхности малого поршня гидравлического пресса 4 квадратных...
3 - ABC подобен треугольнику DEF коэффициента подобия равным 1.6...
1 - Какой была нагрузка приложенная к проволоке ,если ее относительное...
3 - Тигр злопамятен: он легко запоминает запах человека ,его голос ,дожидается...
1 - Выпишите, раскрывая скобки, предложения, в которых вы деленные слова...
1 - 3y^2+7y+4 09у^2-6у+1 03у^2-6у+3 0решите...
2 - В 150 г волы растворили 50 г серной кислоты. Вычислите массовую долю...
3
1)y'=(x⁷/²)'=(7x⁵/²)/2=3.5*x²√x, по формуле производной степенной функции у'=(xⁿ)'=n*xⁿ⁻¹
2)y'=-1/3-производная х равна 1, константа выносится за знак производной.
3)y'=-2/cos²x -табличный, константу вынесли за знак производной.
4) y'=10x⁹-3-производные степенной функции. см. выше.
5) y'=0 - производная константы равна нулю.
Пользуемся правилами дифференцирования функций и таблицей производных .