Найдите все целые значения параметра

Решим квадратное уравнение х=((2а-3)±√(4а²+9-12а-4а²+12а+40)/2)=

((2а-3)±√49)/2; х=а-5; х=а+2

1) (а-5)²-1<0; (а-6)*(а-4)<0, решим неравенство методом интервалов

__46

+        -            +

а∈(4:6) Целое значение параметра а = 5

2)  (а+2)²-1<0; (а+3)*(а+1)<0, решим неравенство методом интервалов

__-3-1

+        -            +

а∈(-3:-1) Целое значение параметра а = -2

Если подставить в уравнение значение а=5;/ аналогично а=-2/, то получим х²-7х+25-15-10=0;

х²-7х=0; х*(х-7)=0 два корня, меньший нуль. удовлетворяет неравенству

0²-1<0

ответа=5; а=-2

По теореме Виета

Меньший корень уравнения удовлетворяет неравенству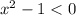 или записав в виде 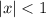. Имеем два случая.

В случае когда оба корня по модулю меньше 1 таких параметров нет. Объединив все решения, получаем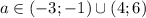 . Целые значения параметра а: -2; 5.