Найдите уравнение прямой медианы bm треугольника abc, если координаты вершин треугольника a(2; 1), b(7; -2), c(5,0)

Ответы

nvgaponuk 09.10.2020 14:41

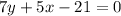
ответ: 7y+5x-21=0

Пошаговое объяснение:

Найдем координаты точки M - середины между точками A и C

M = ((5 + 2) / 2; (0 + 1) / 2) = (7/2; 1/2)

Уравнение прямой проходящей через точки (x1; y1) и (x2; y2) задается формулой:

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$

Для точек B и M получим:

$\frac{x-7}{\frac{7}{2}-7}=\frac{y+2}{\frac{1}{2}+2}\\\frac{x-7}{-\frac{7}{2}}=\frac{y+2}{\frac{5}{2}}\\-7y-14=5x-35\\7y+5x-21=0$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Dudos213 26.04.2020 15:28

alina97531 26.04.2020 15:28

найти сумму корней уравнения 5(х-1,2)=4х-5,2 и 8-3,7х=12+1,3х...

rbhz 26.04.2020 15:28

Определите ординату данной точки А(3;-2)...

айз14 26.04.2020 15:28

EnglishGod 26.04.2020 15:27

Vlad29rus228999 26.04.2020 15:28

хитМо 04.07.2019 07:00

Решите уравнение: 951 - (х - 354) = 882; 549 - (425 - х) = 488...

3твиттер3 04.07.2019 07:00

L1O2N3D4O5N 04.07.2019 07:00

Zulik007 04.07.2019 07:00

Из числа 12 вычти сумму чисел 3 и 5...