Найдите угол между векторами
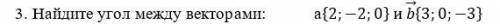
Другие вопросы по теме Математика
Популярные вопросы
- Нужно составить список что можно делать на кухне а что нельзя.2столбика...
2 - Какая масса соли образуется вследствие нейтрализации калий гидроксида...
3 - Наша семья решила сделать ремонт. решили обклеить стены в комнате бордюром....
1 - 3.45 высота и 17.3 ширина, сколько это будет в квадратных метрах...
2 - Аравнобредренном треугольнике авс угол в равен 50© найдите два остальные...
3 - Прочитайте слова. определите форму числа существительных. молодежь....
1 - Утроив магазине было 30 шкафов для книг и 10 шкафов для одежды к концу...
1 - Найдите наименьшее значение функции f(x)=x^3-3x на отрезке [0; 3]...
3 - Что тяжелеет килограмм ваты или железа...
2 - Внекотором году понедельников было больше, чем вторников, а воскресений...
2
или
Пошаговое объяснение:
Обозначим искомый угол как
Тогда угол можно выразить через скалярное произведение и длины векторов:
Итак,
Однако, угол м/ду векторами может принимать значения от 0 до 180° или от 0 до "Пи"
или