Найдите произведение корней уравнения
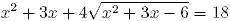
Другие вопросы по теме Математика
Популярные вопросы
- Как по второму закону Ньютона рассчитать силу под действием которой тело...
1 - Сделать характеристику физико-географического положения стран (Великобритания...
3 - Найди числовое значение А и В....
1 - Please choose the most appropriate answer for each sentence. 1. The castle...
1 - ів! Поміркуйте, якими речовинами можна замінити метали....
3 - Здравствуйте, решите пример не могу найти корень : 14x+x+9x-2=70...
3 - Число а составляет 2/5 числа b на сколько процентов b больше а ...
3 - Приведите исторические примеры, которые показывают, что : А). Составные...
1 - от каких налогов не спрячешься?...
2 - Яким було повсякденне життя українців у XVI—XVIII ст.?...
1
x² + 3x + 4√(x² + 3x - 6) = 18
ОДЗ подкоренное выражение корня четной степени >= 0 для действительных корней
x² + 3x - 6 ≥ 0
D = b² - 4a = 9 + 24 = 33
x12 = ( -3 +- √33)/2
[ ( -3 - √33)/2] [ ( -3 + √33)/2]
x ∈ (-∞, ( -3 +- √33)/2] U [ ( -3 + √33)/2, +∞)
( -3 - √33)/2 ≈ - 4.38
( -3 + √33)/2 ≈ 1.37
x² + 3x + 4√(x² + 3x - 6) = 18
x² + 3x - 6 + 4√(x² + 3x - 6) = 12
√(x² + 3x - 6) = t >= 0 (квадратный корень ≥ 0)
t² + 4t - 12 = 0
D = 16 + 48 = 64
t12 = (-4 +- 8)/2 = -6 2
t1 = -6 ≤ 0 не проходит
t2 = 2
√(x² + 3x - 6) = 2
x² + 3x - 6 = 4
x² + 3x - 10 = 0
D = 9 + 40 = 49
x12 = (-3 +- 7)/2 = -5 2
корни -5 2 входят в одз
x1*x2 = -5 * 2 = -10
x1 = -5; x2 = 2;
Пошаговое объяснение: