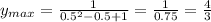Найдите наибольшее значение функции 9^х \ 4^х - 6^х + 9^х и точку х, при которой это значение достигается. (п.с. степень представлена х-ом, привыкла решать через производную, а тут как-то по-другому, можно сделать замены 3^x и 2^x, но что это может
Другие вопросы по теме Математика
Популярные вопросы
- Вряду веществ углекислый газ, поваренная соль, азот, четырёххлористый...
3 - Один из смежных углов в 8 раз меньше другого. найти эти углы....
3 - Объем 1 моль водорода в сосуде при темтерату t и давлении p равен v1....
1 - Хеелп автомобиль выехал с постоянной скоростью 66 километров час из...
3 - Основные темы и проблемы творчества а.н. островского....
3 - Группа из 8 женщин и 2 мужчин, случайным образом садится за стол. найти...
1 - Разность двух внутрених одностороних углов при двух параллельных прямых...
3 - Когда появляется 3d 0 ( т.е 3d в степени 0) при составлении электронной...
3 - Как правильно писать слово занесло за...
1 - Вычислите 2arc sin (-√3/2)+arc tg 1...
3
рассмотрим функцию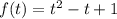 , по свойствам ее минимальное значение достигается в вершине параболы (минимальное так как коэффициент при t равен a=1>0)
, по свойствам ее минимальное значение достигается в вершине параболы (минимальное так как коэффициент при t равен a=1>0)
т.е. при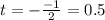
далее рассмотрим функцию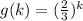 -функция убывающая, поэтому чем меньше ее значение тем меньше ее значение
-функция убывающая, поэтому чем меньше ее значение тем меньше ее значение
далее рассмотрим функцию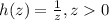 - функция убывающая, чем меньше значение z тем большее значение h(z)
- функция убывающая, чем меньше значение z тем большее значение h(z)
видим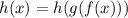 учитывая непрерывность, и все ограничения, видим, что наибольшее значение данной функции достигается при
учитывая непрерывность, и все ограничения, видим, что наибольшее значение данной функции достигается при
а наибольшее значение учитывая что для него выполняется соотношение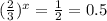
будет