Найдите множество значений функции g(x)= корень из (х^2-10х+34) 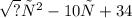
Другие вопросы по теме Математика
Популярные вопросы
- Расставь прилагательные в правильном порядке)) (а где номер 35 36 37...
1 - Обозначьте какие-то точки О,А и В. 1) ОА=2оа, ОВ=2ов; 2) ОА=3оа, ОВ=3ов;...
3 - «Истоки казахского народа. Достижения РК в экономике» 1.Кто жил на...
3 - Erganzt die satze ferienlager....
2 - Прочтите третью строфу укажите образ персонаж который появляется в...
2 - Прогрессивное значение наполеоновских войск...
2 - Найдите первый член и разность арифметической прогрессии...
1 - 4. Выпишите средства художественной выразительности из данного отрывка....
1 - Составите сочинения 10-12 предложении о царе Хаммурапи и о городе Вавилон...
2 - Прочитай текст. Какая пословица соответствует теме текста? Незваного...
3
Нам дана функция g(x) = √(x^2 - 10x + 34).
Мы должны найти множество значений этой функции, то есть все возможные значения g(x).
Прежде чем продолжить, давайте вспомним некоторые важные свойства корней квадратных уравнений:
1. Корни квадратного уравнения всегда являются действительными числами.
2. Если a^2 ≥ 0, то √a^2 = |a|, где |a| - абсолютное значение числа a.
Теперь, чтобы найти множество значений функции g(x), нам нужно найти все значения выражения x^2 - 10x + 34 и взять их корни.
Для начала, посмотрим, какое значение может принимать выражение x^2 - 10x + 34:
1. Определитель D = (-10)^2 - 4 * 1 * 34 = 100 - 136 = -36.
Поскольку D < 0, это означает, что выражение x^2 - 10x + 34 не имеет действительных корней.
Следовательно, у нас нет вещественных значений функции g(x), значит, множество значений функции g(x) пусто.
Ответ: Множество значений функции g(x) пусто.