1. Математика
  2. Найдите частное решение

Найдите частное решение удовлетворяющее заданному начальному условию x^2y'+y^3=0 ; y(0,5)=1

Катттття Катттття    3   19.09.2019 06:50    3

Ответы
LarisaSergeeva LarisaSergeeva  08.10.2020 01:40
ДУ с разделяющимися переменными.
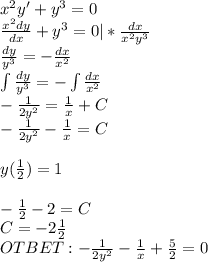
x^2y'+y^3=0\\\frac{x^2dy}{dx}+y^3=0|*\frac{dx}{x^2y^3}\\\frac{dy}{y^3}=-\frac{dx}{x^2}\\\int\frac{dy}{y^3}=-\int\frac{dx}{x^2}\\-\frac{1}{2y^2}=\frac{1}{x}+C\\-\frac{1}{2y^2}-\frac{1}{x}=C\\\\y(\frac{1}{2})=1\\\\-\frac{1}{2}-2=C\\C=-2\frac{1}{2}\\OTBET:-\frac{1}{2y^2}-\frac{1}{x}+\frac{5}{2}=0
ПОКАЗАТЬ ОТВЕТЫ
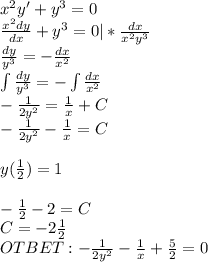
Другие вопросы по теме Математика
14andrew 14andrew  11.05.2020 16:45
S сверху 3 снизу -2 (4x^3-3x^2+2x+1)dx​...
rudembatalov rudembatalov  11.05.2020 16:46
Множество решений неравенства tg(2x-П/3) √3 /3 принадлежит промежутку...
slaviktaran00 slaviktaran00  11.05.2020 16:46
10. Что такое определитель 3-го порядка? а. вектор, координатами которого являются элементы, стоящие на главной диагонали матрицы; б. вектор, координатами которого являются...
jpjpjp jpjpjp  11.05.2020 16:46
Как решать круговые примеры....
Valerivaleeva Valerivaleeva  11.05.2020 16:46
найдите значение выражения 6a 2+3ab 2-4ab-2b 3 , если а=одна целая одна восьмая. b=-одна целая 1 вторая...
nastyap20032 nastyap20032  11.05.2020 16:46
1.Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик. 2.Девятиклассники Петя, Катя,...
LoliPeen LoliPeen  11.05.2020 16:46
Скорость скутера по течению реки – 27 км/ч, а против течения – 24 км/ч. Чему равна скорость течения реки? Катя и Сергей одновременно отправились навстречу друг другу. Катя...
katalkina17 katalkina17  11.05.2020 16:46
Через точку К, що лежить поза прямой c, проведить пряму A) Паралельну прямий c, B) Берпендекулярну прямий c,...
angeldeikina angeldeikina  18.09.2019 13:40
За 3ч художник расписал 4 вазы. сколько времени ему потребуется,чтобы расписать 20 ваз, если он работает с одинаковой скоростью?...
Fosa1 Fosa1  18.09.2019 13:40
Три самые известные музыкальные группы в южной корее надо...

Популярные вопросы