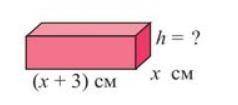
На рисунке указаны размеры основания прямоугольного параллелепипеда. Найдите
высоту параллелепипеда, если объём равен
(x^3 + 5x^2 + 6x) cm^3
Другие вопросы по теме Математика
Популярные вопросы
- У чому полягала суперечливість зовнішньої політики перших кримських...
3 - Только мне нужен ответ в первый столбик примера и во второй...
3 - Из какого числа надо вычесть 520, чтобы получилось 150? ( знаю...
1 - Обчислить масову частку цуару в розчини, одержаному розчиненям...
2 - 1. Как в рассказе отражено2. Расположите части рассказа в правильном...
1 - Прочитайте предложения. Обратите внимание на союзы: какие это...
2 - Розвязати рівняння -0,12=0,3х-1,4х-1,1х...
1 - 1. Определите общее сопротивление цепи, если R1=2 Ом, R2=3 Ом,...
2 - Что произойдет, если по проводнику, помещённому в магнитное поле,...
2 - Перевести обыкновенную дробь 11/3 в десятичную с периодом!!...
3
Объем = длина * ширина * высота
Следовательно, нам нужно найти значение высоты. Известно, что объем равен (x^3 + 5x^2 + 6x) cm^3, и размеры основания прямоугольного параллелепипеда уже даны на рисунке. Давайте подставим значения и решим уравнение:
Длина = (x + 2) cm
Ширина = (x + 1) cm
Высота = ?
(x + 2) * (x + 1) * Высота = (x^3 + 5x^2 + 6x) cm^3
Чтобы упростить это уравнение, умножим правую сторону:
Высота * (x^2 + 3x + 2) = x^3 + 5x^2 + 6x
Теперь раскроем скобки:
Высота * x^2 + Высота * 3x + Высота * 2 = x^3 + 5x^2 + 6x
Сгруппируем подобные члены:
x^3 + (5 + Высота) * x^2 + (6 + 3 * Высота) * x + 2 * Высота = 0
Таким образом, у нас получилось кубическое уравнение, которое мы можем решить.
Однако, увидев коэффициенты при x^3 и x^2, мы можем предположить, что у нас есть корень (x = -1), так как факторизация в основном используется, когда у нас есть корень.
Теперь мы знаем, что (x + 1) является одним из множителей, давайте разделим уравнение на (x + 1):
(x + 1)(x^2 + (5 + Высота) * x + (6 + 3 * Высота)) = 0
Теперь, рассмотрим второй множитель. Чтобы найти значение высоты, нужно сделать дополнительное предположение о том, что (x^2 + (5 + Высота) * x + (6 + 3 * Высота)) = 0 имеет корни, которые помогут нам найти значение высоты.
Мы можем исследовать это уравнение с помощью квадратного трехчлена, который выглядит следующим образом:
x^2 + px + q = 0, где p = 5 + Высота и q = 6 + 3 * Высота
Давайте найдем корни этого квадратного трехчлена, используя формулу:
x = (-p +- sqrt(p^2 - 4 * q)) / 2
Зная значения p и q, подставим и найдем корни.
По сути, мы ищем корни выражения x^2 + (5 + Высота) * x + (6 + 3 * Высота) = 0, но так как это предположение, то давайте оставим его в таком виде.
Подставим корни в уравнение, чтобы получить возможные значения высоты:
(x + 1)(x - корень)(x - корень) = 0
Когда мы подставим корни в это уравнение, мы найдем две возможные высоты параллелепипеда.
Теперь, осталось только решить это уравнение и найти корни. К сожалению, я не могу вычислить корни и получить конкретные значения высоты, не зная конкретных значений коэффициентов в уравнении.
Надеюсь, что пошаговое решение поможет вам справиться с этой задачей! Если у вас возникли дополнительные вопросы, не стесняйтесь задавать.