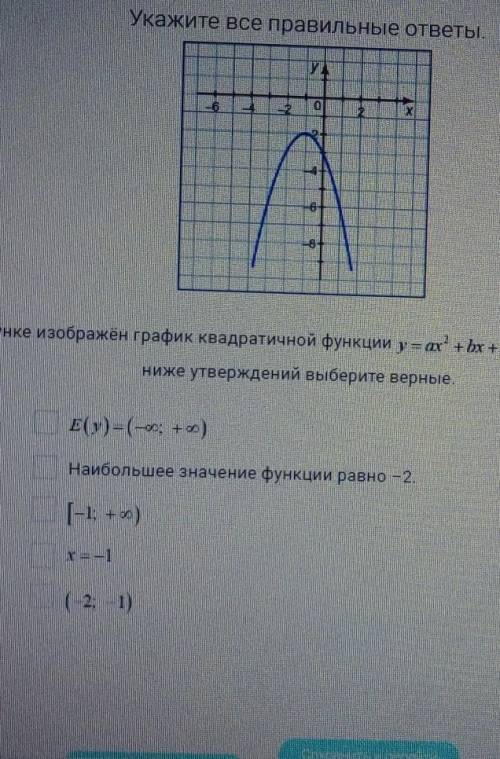
На рисунке изображён график квадратичной функции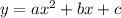
Из приведённых ниже утверждений выберите верные
​

Утверждение 1: График функции проходит через точку A (0, -3).

Для проверки данного утверждения, мы должны проверить, что если мы подставим x = 0 в уравнение функции, то получится y = -3.

Подставляем x = 0 в уравнение функции:
y = a * (0^2) + b * 0 + c
y = 0 + 0 + c
y = c

Таким образом, если график проходит через точку A (0, -3), то значение функции при x = 0 должно быть -3, следовательно, c = -3.

Утверждение 2: График функции пересекает ось ординат в точке B (0, 2).

Для проверки данного утверждения, мы должны проверить, что значение функции при x = 0 равно 2.

Подставляем x = 0 в уравнение функции:
y = a * (0^2) + b * 0 + (-3)
y = 0 + 0 - 3
y = -3

Таким образом, если график пересекает ось ординат в точке B (0, 2), то значение функции при x = 0 должно быть 2, что не соответствует уравнению функции.

Утверждение 2 неверно.

Утверждение 3: График функции имеет вершину, лежащую выше оси абсцисс.

Чтобы найти вершину графика квадратичной функции, мы можем использовать формулу x = -b / (2a) для нахождения абсциссы вершины и подставить полученное значение абсциссы вершины в уравнение функции для нахождения ординаты вершины.

В данном случае, уравнение функции y = ax^2 + bx + c, где a = 1, b = -2 и c = -3.

Находим абсциссу вершины графика:
x = -(-2) / (2 * 1)
x = 2 / 2
x = 1

Теперь подставим полученное значение x = 1 в уравнение функции для нахождения ординаты вершины:
y = 1 * (1^2) - 2 * 1 - 3
y = 1 - 2 - 3
y = -4

Таким образом, вершина графика функции находится в точке (1, -4), что означает, что она лежит ниже оси абсцисс.

Утверждение 3 неверно.

Итак, верными утверждениями являются только утверждение 1 и утверждение 2 неверно.