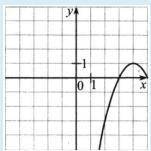
На рисунке изображён график функции вида y = ax^2+bx+c, где числа a, b и с - целые. Найдите у(-19).

Данная функция является квадратичной, и ее график — это парабола.

Сперва нужно определить коэффициенты а, b и c в формуле функции.

Формула абсциссы вершины параболы:

По графику видим, что абсцисса вершины равна 4.  

Значит, .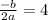

Выберем две точки с целочисленными координатами, принадлежащие параболе.

Возьмем вершину, т. А (4; 1) и т. В (2; -3).

Подставим координаты точек в формулу функции: абсциссу вместо х, а ординату вместо у.

Получаем два уравнения:

1)

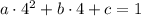
2)

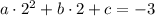
Составим систему уравнений:

Из первого уравнения выразим коэффициент b.

Сперва умножим обе части уравнения на знаменатель дроби:

Теперь умножим обе части на -1:

Из второго уравнения вычтем третье, чтобы избавиться от коэффициента c. Отдельно вычитаем левые, отдельно правые части:

Раскроем скобки:

Приведем подобные слагаемые:

Разделим обе части уравнения на 2 для удобства:

Подставим значение коэффициента b:

Теперь найдем коэффициент b, подставив найденное значение коэффициента а в уравнение :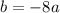

Подставим значения коэффициентов а и b в третье уравнение системы, чтобы найти коэффициент с:

Подставим найденные коэффициенты в формулу функции:

у = -х² + 8х - 15

Чтобы найти у(-19), подставим число -19 вместо аргумента:

ответ: -528.