На каком расстоянии от фонаря ( в метрах) стоит человек ростом 1,8 м, если длина его тени равна 9 м, а высота фонаря 5 м?

Получаются подобные треугольники.

пусть расстояние между фонарем и человеком Х,

тогда составим пропорцию:

1,8/5 = 9/ (х+9).

Отсюда, найдем Х:

х+9=9*5/1,8

х+9=25

х=16м - расстояние между фонарем и человеком

ответ. 16м

Пусть CD - человек, AB - фонарь, CF - тень человека

Тогда: CD=1,8; AB=5; CF=9

Требуется найти: AС

1) Рассмотрим треугольники ABF и CDF - они подобны (общий угол F и равные углы FCD и FAB (прямые))

2) Из подобия следует отношение сторон:

Подставим известные значения:

Найдём AF: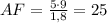

AC=AF-CF=25-9=16