На доске написано 6 различных цифр.ученик составил из них наибольшее из возможных чисел, используя каждую цифру один раз.затем он разделил это число на 10 и из цифр частного составил новое число,расположив цифры в обратном порядке.запишите шестизначное число,которое составил ученик,если каждая следующая цифра перевёрнутого частного обозначает число,отличающееся от предыдущего на 2. решение и ответ.
Другие вопросы по теме Математика
Популярные вопросы
- Функции заданы формулами f(x)=x2+1 и g(x)=x2−1. Сравни f(3) и g(8)....
1 - При каких значениях b и c график функции y = x² + bx + c проходит через точки...
2 - Какой алгоритм следует использовать для создания рисунка с повторяющимся узором?...
2 - Звездный треугольник Напишите программу, которая выводит указанный треугольник,...
3 - Изучите правила составления родословных. Попробуйте вместе с родителями составить...
1 - Який з авторів, згаданих у третій частині підручника, був пов язаний з українською...
3 - В ромбе OPST, где точка N- точка пересечения диагоналей, угол OPS равен 112...
2 - Read the poem. Who is it about? are fast. are cool. They watch all the kids...
2 - Большой мотор EV3 является более мощным, чем средний мотор EV3. Это происходит...
1 - Найти график функции: y=3x^2-5+5...
2
Итак, наше число делится на 10(исходя из 3его предложения в условии), а значит и заканчивается на 0. Тогда оно имеет вид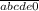 , откуда перевернутое частное выглядит как
, откуда перевернутое частное выглядит как 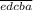 .
.
Так как цифры отличаются на 2, то все они одной четности. В нашем распоряжении осталось 4 четных(0 ведь уже был использован) и 5 нечетных. Очевидно, что наше 5и-значное число, состоящее из различных цифр(так как при делении на 10 числа, кратного 10, отбрасывается 0), либо 13579, либо 97531.
Значит искомое число 975310 или 135790
Учитывая, что было составлено наибольшее из возможных чисел, то число равно 975310