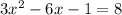Можете объяснить что и в каком порядке нужно найти, чтобы найти нужные значения х.
Другие вопросы по теме Математика
Популярные вопросы
- 3 -тапсырма.Суретке қара. «Ғаламтордың тұңғиығы»тақырыбында ғаламторды пайдала-ну...
2 - Определи, к какому уровню организации относятся следующие при меры:сердцестадо...
1 - Электрическая цепь составлена из резисторов сопротивления которых равны: R1=8...
1 - Выполните тест открытого типа, дополните недостающие ответы из текста 1. Какой...
3 - Синус 6 альфа*косинус 2 альфа-синус 2 альфа*косинус 6 альфа - спростити вираз...
3 - Вот напишите с если сос сос сос✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅...
2 - ким приладом вимірюється напруга і яким чином він приєднується до ділянки...
3 - Существительные на букву P 1 и 2 склонения латинский язык...
3 - Які тереторії стародавнього Китаю молопредатні для зайнятості землеробству?...
1 - 1. Write the verbs in Present Simple. пртеTom s father1. Tom s father2. His...
2
f(x) и y это одно и то же.
f'(x) означает, что нужно найти первую производную
f(2) означает, что нужно найти значение функции при х=2
Далее вы получите уравнение, которое вам нужно будет решить, чтобы найти x.
Пошаговое объяснение:
f'(x) = f(2) ⇒