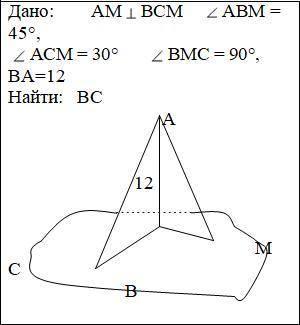
Математика ( геометрия ) 10 класс решить! Дано: АМ ВСМ АВМ = 45°,
АСМ = 30° ВМС = 90°, ВА=12
Найти: ВС

Для решения данной геометрической задачи, мы можем использовать свойства треугольника и теорему синусов.

Из условия задачи видно, что угол AMV равен 45°, угол ASM равен 30° и угол VMS равен 90°. Также дана длина отрезка VA, равная 12.

Первым шагом для решения задачи мы можем найти длину отрезка AM, используя тригонометрическую функцию синус. Мы знаем, что синус угла равен отношению противолежащего катета к гипотенузе. Поэтому, с помощью синуса угла AMV, мы можем записать следующее уравнение:

sin(45°) = AM / VA

Решим это уравнение относительно AM:

AM = VA * sin(45°) = 12 * 0.707 ≈ 8.485

Теперь, когда у нас есть длина отрезка AM, мы можем использовать свойство прямоугольного треугольника исоскелья, чтобы найти длину отрезка VM. Мы знаем, что в прямоугольном треугольнике два катета равны и гипотенуза равна произведению длин катетов на √2. Поэтому отрезок VM равен:

VM = AM * √2 = 8.485 * 1.414 ≈ 12

Теперь для дальнейшего решения задачи нам необходимо найти отрезок CS. Мы можем использовать тригонометрическую функцию синус и теорему синусов для этого:

sin(30°) = CS / VM

Решим уравнение относительно CS:

CS = VM * sin(30°) = 12 * 0.5 = 6

Таким образом, получаем, что длина отрезка CS равна 6.

Наконец, чтобы найти искомую длину отрезка VS, мы можем использовать свойство прямоугольного треугольника исоскелья. Длина отрезка VS равна гипотенузе этого треугольника. Поэтому длина отрезка VS будет равна:

VS = VM = 12

Таким образом, ответ на задачу состоит в том, что длина отрезка ВС равна 12.