Лф6) Вычислить: [ 3^(1+log4(5))×4^(log5(3))×5^(log3(4)) ] ÷ [ 3^(log5(4)) × 4^(log3(5)) × 5^(log4(3)) ] В понятном виде:
Заранее большое
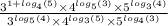
Другие вопросы по теме Математика
Популярные вопросы
- Решите графически систему уравнений y=x^2 y=-x+2...
1 - Масса грузового автомобиля в 6 раз больше массы легкового автомобиля....
3 - Два товароведа расположили девять мотков пряжи в порядке убывания...
2 - Подскажите часть речи слова освобождено(...
3 - Вычислил площадь фигуры, ограниченной линиями xy=4, x=1, y=0...
3 - 1яйцо жарится 3 минуты. сколько жарится 5...
3 - Первую половину беговой дорожки спортсмен пробежал со скоростью...
3 - Старовинна : учень на запитання, скільки йому років , відповів:...
1 - Вычислил площадь фигуры, ограниченной линиями xy=4, x=1, y=0...
3 - Сколько анаграмм у слова обморок?...
2
Пошаговое объяснение: